线性微分系统的反射函数及小参数扰动

考虑线性微分系统

这里P（t）为n×n阶连续的矩阵函数，t∈R，x∈Rⁿ.

我们知道^[2-3]，若P（t+2ω）=P（t），则存在非奇异的Lyapunov变换

x=Φ（t）y，Φ（t+2ω）=Φ（t），

将式（3.4.1）化为

这里B为n×n阶常数矩阵，则系统（3.4.1）满足x（t₀）=x₀的解可表示为

x=Φ（t）expB（t-t₀）Φ^-1（t₀）x₀，

从而系统（3.4.1）的反射矩阵为

F（t）=Φ（-t）exp（-2Bt）Φ^-1（t）. （3.4.2）

下面我们首先讨论对于任一个线性系统（3.4.1）何时具有形如

F（t）=e^Ate^Bte^At （3.4.3）

的反射矩阵？这里A为n×n阶常数矩阵.本节中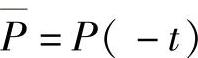，D=D（-t）等等.

引理3.4.1 若F（t）=e^Ate^Bte^At为系统（3.4.1）的反射矩阵，则B=-2（A+P（0）），且

2（P²（0）A-2P（0）AP（0）+AP²（0））-（A²P（0）-2AP（0）A+P（0）A²）+

2（P′（0）P（0）-P（0）P′（0））+P″（0）=0. （3.4.4）

证 由于F=e^Ate^Bte^At为系统（3.4.1）的反射矩阵，则

即

记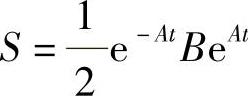，则上式可写为

记D=A+S+P，则

在式（3.4.6）中令t=0得D（0）=0，即

B=-2（A+P（0））.

将式（3.4.5）求导两次得

由式（3.4.5）得，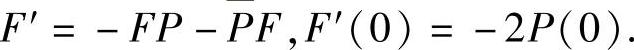

又

则

D′（0）=S′（0）+P′（0）=A（A+P（0））-（A+P（0））A+P′（0）=AP（0）-P（0）A+P′（0），

D″（0）=S″（0）+P″（0）=A²（A+P（0））-（A+P（0））A²+P″（0）=A²P（0）-P（0）A²+P″（0）.

在式（3.4.7）中取t=0得

F′（0）D′（0）+D″（0）-D′（0）F′（0）=0，

即

-2P（0）（AP（0）-P（0）A+P′（0））+A²P（0）-P（0）A²+P″（0）+2（AP（0）-P（0）A+P′（0））P（0）=0，

整理即得式（3.4.4）.

定理3.4.1 若P（t）=e^-Ate^{（A+P（0））t}Q（t）e^{-（A+P（0））t}e^At_+e-^AtP（0）e^At，

（3.4.8）

则微分系统（3.4.1）的反射矩阵为

F（t）=e^Ate^{-2（A+P（0））t}e^At， （3.4.9）

这里Q（t）为任意的连续奇矩阵函数，A是一个n×n阶常数矩阵.

反之，若系统（3.4.1）的反射矩阵为式（3.4.9），则一定存在奇连续矩阵函数Q（t）使得P（t）可由式（3.4.8）表示.

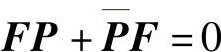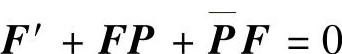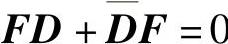证 若P（t）由式（3.4.8）表示，我们很容易验证对于矩阵（3.4.9）成立F′+，F（0）=E，即F（t）为系统（3.4.1）的反射矩阵.反之，若式（3.4.9）为系统（3.4.1）的反射矩阵，则，即，即

令 Q（t）：=e^{-（A+P（0））t}e^AtDe^-Ate^{（A+P（0））t}，则由上式可推得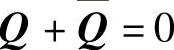，即Q（t）为奇连续矩阵函数，则

定理3.4.2 若P（t）可由式（3.4.8）表示，且P（t+2ω）=P（t），则

1）周期系统（3.4.1）的Poincare′映射为

F（-ω，x）=e^-Aωe^{2（A+P（0））ω}e^-Aωx；

2）系统（3.4.1）的解x=φ（t；-ω，x₀）为2ω-周期，当且仅当，x₀为F（-ω，x）的不动点，即F（-ω，x₀）=x₀；

3）对于系统（3.4.1）的任一解x（t），向量函数y（t）=e^{-（A+P（0））t}e^Atx（t）为t的偶函数.

证 由定理3.4.1知，矩阵（3.4.9）为系统（3.4.1）的反射矩阵，由第2章引理2.1.1即可直接导出定理的结论1）和2）.

下面证明结论3）成立.由反射函数的性质F（t，x（t））=x（-t）得

x（-t）=e^Ate^{-2（A+P（0））t}e^Atx（t），

由此得

e^-Atx（-t）=e^{-2（A+P（0））t}e^Atx（t），

e^{（A+P（0））t}e^-Atx（-t）=e^{-（A+P（0））t}e^Atx（t），

即y（t）=y（-t）.

引理3.4.2 若P（t）可表示为

P（t）=e^-AtP（0）e^At+r（t）E， （3.4.10）

其中A为n×n阶常数矩阵，r（t）为奇的连续纯量函数.则系统（3.4.1）的反射矩阵为

F（t）=e^Ate^{-2（A+P（0））t}e^At.

该引理只要在定理3.4.1中取Q（t）=r（t）E即可得.

若P（t）=e^-AtP（0）e^At，此时引理3.4.1的结论也正确.

一般情况下，一个周期函数可以展开成傅里叶级数，在此我们讨论

P（t）=A₁+B₁cosmt+C₁sinmt+B₂cosrt+C₂sinrt， （3.4.11）

其中A₁，B₁，C₁，B₂，C₂为n×n阶常数矩阵，m，r为实数.

定理3.4.3 若P（t）由式（3.4.11）表示，m≠0，则系统（3.4.1）中的矩阵可

表示为

P（t）=e^-AtP（0）e^At， （3.4.12）

当且仅当

证 必要性 设矩阵（3.4.11）可表示成式（3.4.12），两边求导得

P′=-AP+PA，

P（k）=P^（k-1）A_-AP^（k-1），∀k∈N.

将τ=mt代换t可得

即

在上式取τ=0得

由式（3.4.14）d可推导，s=k+1，k+2，…

即

由此可推得AC₂-C₂A=rB₂.同理从式（3.4.14）e可推得B₂A-AB₂=rC₂.应用这些等式及式（3.4.14）d和式（3.4.14）e得到AC₁-C₁A=mB₁，B₁A-AB₁=mC₁.从式（3.4.14）_a得A₁A=AA₁.因此式（3.4.13）成立.

充分性 假设条件（3.4.13）成立，且P（t）由式（3.4.11）表示，则可以验证，对∀k∈N有

记Q（t）：=e^-AtP（0）e^At.由前面推导得对于k∈N⁺，有

由于Q（0）=P（0），则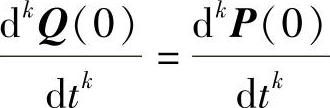.由于函数P（t），Q（t）是解析的，从而P（t）≡Q（t）.即充分性成立.

现在将上述结论应用于研究含小参数的非线性2ω-周期系统解的性态.

考虑含参数微分系统

其中f是关于t的连续的2ω-周期向量函数，ε很小，且f关于x连续可微.设x=g₀（t）为系统（3.4.15）当ε=0时的2ω-周期解.

定理3.4.4 假设F=e^Ate^{-2（A+P（0））t}e^At为线性微分系统

的反射矩阵.其中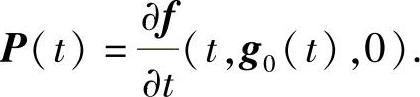

若特征方程

det（e^-Aωe^{2（A+P（0））ω}e^-Aω-μE）=0不存在单位根，则当ε＜＜1时，微分系统（3.4.15）存在唯一2ω-周期解x=x（t，ε），并且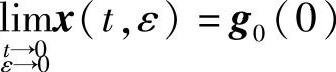.而且x（t，ε）关于（t，ε）连续且x（t，0）=g₀（t）.又若f关于ε连续可微，则x（t，ε）也关于ε连续可微.

证 由于2ω-线性系统（3.4.16）的特征乘子为特征方程

det（e^-Aωe²（^{A+P（0））ω}e^-Aω-μE）=0的根.其它结论可参考文献[13]中的定理2.3推得.

当系统（3.4.15）为拟线性系统

这里P（t）为连续的2ω-周期矩阵，f（t）和φ（t，x）是关于t，x的连续可微的2ω-周期向量函数，ε为小参数.

由定理3.4.4可推出下面定理

定理3.4.5 假设F（t）=e^Ate^{-2（A+P（0））t}e^At为线性系统x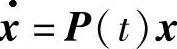的反射矩阵，特征方程det（e^-Aωe^{2（A+P（0））ω}e^-Aω-μE）=0不存在单位根，则当ε＜＜1时，微分系统（3.4.17）存在唯一2ω-周期解x=x（t，ε）并且满足(https://www.daowen.com)

这里x₀（t）为线性系统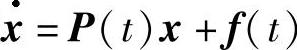的一个2ω-周期解.当系统（3.4.15）为自治系统

这里f关于小参数ε连续，关于x连续可微.设x=η（t）≠常数向量，它是微分系统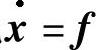（x，0）一个2ω₀-周期解，与定理3.4.5同理可得：

定理3.4.6 假设矩阵F（t）=e^Ate^{-2（A+P（0））t}e^At为线性系统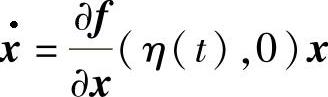的反射矩阵.又若特征方程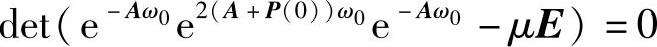存在唯一一个单位根（且为单根），则对充分小的ε微分系统（3.4.17）存在唯一一个2ω（ε）-周期解x=x（t，ε）且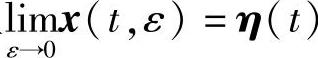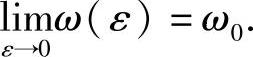，参考文献[13，P488]定理2.4可得.

例3.4.1 考虑拟线性π-周期系统

这里f₁（t），f₂（t），φ₁（t，x，y），φ₂（t，x，y）为关于t的连续的π-周期函数，φ₁（t，x，y），φ₂（t，x，y）关于x，y连续可微，ε为小参数.

可以验证

且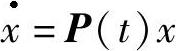的反射矩阵为

其中

特征方程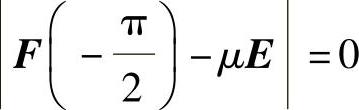的根为

由定理3.4.4推得，对于充分小的ε，微分系统（3.4.19）存在唯一π-周期解.

例3.4.2 考虑系统

这里f₁，f₂关于ε连续，关于x，y连续可微，且

当ε=0时，x₀=sint，y₀=cost为系统（3.4.20）_ε=0的2π-周期解.相应的线性变分系统为

由引理3.4.2得系统（3.4.21）的反射矩阵为

则变分系统（3.4.21）的特征乘子为μ₁=1，μ₂=e^-4π.由定理3.4.6得，对于充分小的ε，微分系统（3.4.20）存在唯一2ω（ε）-周期解：x=x（t，ε），y=y（t，ε），且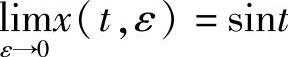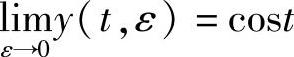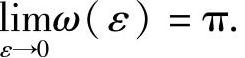，，并且这个解及周期ω（ε）连续，x（t，0）=sint，y（t，0）=cost，ω（0）=π.

现在讨论线性系统（3.4.1）何时以

F（t）=e^A（-t）e^2Bte^-A（t） （3.4.22）

为反射矩阵^[125].这里B为n×n阶常数矩阵，A（t）为可微矩阵函数.

定理3.4.7F（t）=e^A（-t）e^2Bte^-A（t）为系统（3.4.1）的反射矩阵，当且仅当，

FD（t）+D（-t）F=0， （3.4.23）

B=e^-A（0）（A′（0）-P（0））e^A（0）， （3.4.24）

这里D（t）：=e^A（t）Be^-A（t）+P（t）-A′（t）.

证 式（3.4.22）为系统（3.4.1）的反射矩阵，当且仅当，

F′（t）+F（t）P（t）+P（-t）F（t）=0，

即

F（t）（e^A（t）Be^-A（t）+P（t）-A′（t））+（e^A（-t）Be^-A（-t）+

P（-t）-A′（-t））F（t）=0，

即

F（t）D（t）+D（-t）F（t）=0，

令t=0得D（0）=0，由此推得式（3.4.24），式（3.4.23）均成立.

定理3.4.8 式（3.4.22）为系统（3.4.1）的反射矩阵，当且仅当，P（t）可表示为

P（t）=A′（t）-e^A（t）Be^-A（t）+e^A（t）e^-BtN（t）e^Bte^-A（t）， （3.4.25）其中N（t）为奇矩阵函数，B由式（3.4.24）表示.

证 由定理3.4.7可得，式（3.4.11）为系统（3.4.1）的反射矩阵，当且仅当，

F（t）D（t）+D（-t）F（t）=0，

即

e^A（-t）e^2Bte^-A（t）D（t）+D（-t）e^A（-t）e^2Bte^-A（t）=0.

由此可推得

e^Bte^-A（t）D（t）e^A（t）e^-Bt+e^-Bte^-A（-t）D（-t）e^A（-t）e^Bt=0.

令N=e^Bte^-A（t）D（t）e^A（t）e^-Bt，则N（t）+N（-t）=0，D=e^A（t）e^-BtNe^Bte^-A（t），由此推出P（t）可由式（3.4.25）表示.

推论3.4.1 若P（t）=A′（t）-e^A（t）Be^-A（t）+r（t）E，则F（t）=e^A（-t）e^2Bte^-A（t）为

系统（3.4.1）的反射矩阵.这里r（t）为任意连续可微的奇的纯量函数，E为n×n阶单位矩阵，B由式（3.4.24）表示.

该结论只要在定理3.4.8中取N=r（t）E即可推得.

推论3.4.2 若P（t）=（α′（t）+r（t）-α′（0））E-P（0），则系统（3.4.1）的反射矩阵为

F（t）=e^-2α（t）e^2Bt，

其中B=α′（0）E+P（0），E为单位矩阵，α（t），r（t）为连续可微的奇的纯量函数.

只要在推论3.4.1中取A（t）=α（t）E即可得出该结论.

定理3.4.9 假设P（t+2ω）=P（t），且式（3.4.22）为系统（3.4.1）的反射矩阵，则

1）F（-ω）x=e^A（ω）e^-2Bωe^-A（-ω）x为系统（3.4.1）在[-ω，ω]上的Poincaré映射；

2）微分系统（3.4.1）的解x=φ（t；-ω，x₀）为2ω-周期解，当且仅当，F（-ω）x₀=x₀；

3）对于系统（3.4.1）的任一解x（t），函数y（t）=e^Bte^-A（t）x（t）为t的偶函数.该定理可与定理3.4.2同理可证.

例3.4.3 微分系统

具有反射矩阵F（t）=e^A（-t）e^2Bte^-A（t），其中

容易验证P（t）=A′（t）-e^A（t）Be^-A（t）成立.由于该线性系统为2π-周期系统，则其Poincaré映射为T（x）=F（-π）x.由于det（F（-π）-E）=（e^-2π-1）2≠0，则当前2π-周期系统存在唯一2π-周期解且渐近稳定.

定理3.4.10 假设

则F（t）=e^A（-t）e^2Bte^-A（t）为系统（3.4.1）的反射矩阵.这里r_k（t），β_k（t）（k=1，2，…，m）为连续可微的奇的纯量函数.M（t）为n×n矩阵函数.B=e^-A（0）（A′（0）-P（0））e^A（0）.

证 由定理3.4.7，我们要证明当前的结论成立，只需验证

F（t）D（t）+D（-t）F（t）=0成立.事实上

记U（t）=F（t）M（t）-M（-t）F（t），则U（0）=0，

又由于F（t）=e^A（-t）e^2Bte^-A（t），则

F′（t）=F（t）（S（t）-A′（t））+（S（-t）-（A（-t））′）F（t）.

这里S（t）：=e^A（t）Be^-A（t），记，则

又U（0）=0，则由一阶线性方程组初值问题解的唯一性得U（t）≡0.从而

从而定理得证.

定理3.4.11 若F（t）=e^-A（t）e^2Bte^-A（t）为系统（3.4.1）的反射矩阵，且A（t）+A（-t）=0.则存在一个奇函数矩阵N（t）使得

e^A（t）（P（t）-P（-t））e^A（t）=Be^2A（t）-e^2A（t）B+e^2A（t）e^-BtN（t）e^Bt+e^BtN（t）e^-Bte^2A（t），

（3.4.26）

其中B=A′（0）-P（0），A′（0）P（0）-P（0）A′（0）=P′（0）-N′（0）.

证 由定理3.4.8知，存在n×n阶奇的矩阵函数N（t）使得

P（t）=A′（t）-e^A（t）Be^-A（t）+e^A（t）e^-BtN（t）e^Bte^-A（t）， （3.4.27）

则

P（-t）=A′（t）-e^-A（t）Be^A（t）-e^-A（t）e^BtN（t）e^-Bte^A（t）， （3.4.28）

将式（3.4.27）减去式（3.4.28）得式（3.4.26）.

由A（t）+A（-t）=0，则A（0）=A″（0）=0.将式（3.4.27）求导并令t=0得

A′（0）P（0）-P（0）A′（0）=P′（0）-N′（0）.

注 若能从等式

A′（0）P（0）-P（0）A′（0）=P′（0）-N′（0）

解出A′（0），并从式（3.4.26）中解出e^A（t），并且e^A（t）满足

（e^A（t））′=P（t）e^A（t）+e^A（t）B-e^A（t）e^-BtN（t）e^Bt.

其中B=A′（0）-P（0），则F（t）=e^-A（t）e^2Bte^-A（t）为系统（3.4.1）的反射矩阵.

与上定理同理可得

定理3.4.12 假设F（t）=e^A（t）e^2Bte^-A（t）为系统（3.4.1）的反射矩阵，且A（t）=A（-t）.则存在一个奇函数矩阵N（t）使得

（P（t）+P（-t））e^A（t）+2e^A（t）B=e^A（t）（e^-BtN（t）e^Bt-e^BtN（t）e^-Bt） （3.4.29）

其中

B=-e^-A（0）P（0）e^A（0），

A″（0）+e^A（0）+e^A（0）N′（0）e^-A（0）=P′（0），

P″（0）=（3A″（0）-2P′（0））P（0）-P（0）（3A″（0）-2P′（0））.

注 若从式（3.4.29）解出e^A（t），则B=-e^-A（0）P（0）e^A（0）已知.又若e^A（t）满足

（e^A（t））′=P（t）e^A（t）+e^A（t）B_-e^A（t）e^-BtN（t）e^Bt，

则F（t）=e^A（t）e^2Bte^-A（t）为系统（3.4.1）的反射矩阵.