微分系统的反射函数及应用

现在我们考虑线性微分系统

这里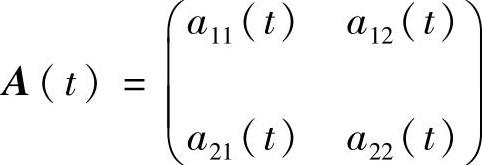为连续矩阵.设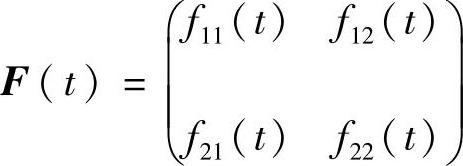为系统（3.3.1）的反射矩阵.

下面我们着重讨论线性微分系统（3.3.1）具有各种特殊类型的反射矩阵的充分条件.在本节中我们简记：

情形Ⅰ

引理3.3.1 若矩阵函数（3.3.2）为反射矩阵，则f₁₁=e^φ11（t），f₂₂=e^φ22（t），φ₁₁（t），φ₂₂（t）为可微的奇函数.

证 由反射矩阵的性质得，若矩阵（3.3.2）为某微分系统的反射矩阵，则，F（-t）F（t）=F（0）=E，即f₁₁（-t）f₁₁（t）=1，f₂₂（-t）f₂₂（t）=1，f₁₁（0）=f₂₂（0）=1.令f₁₁=e^φ11（t），f₂₂=e^φ22（t）则φ₁₁（t）+φ₁₁（-t）=0=φ₂₂（t）+φ₂₂（-t）.

定理3.3.1 对于微分系统（3.3.1）若满足

则其反射矩阵为

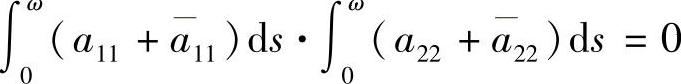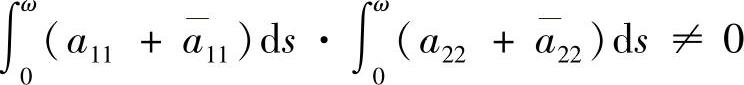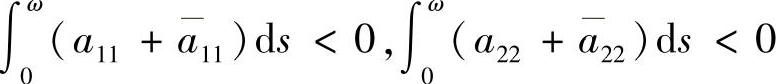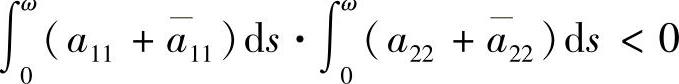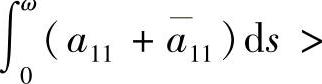
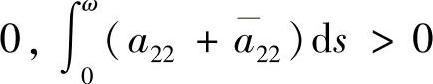若A（t+2ω）=A（t），则当时，系统（3.3.1）具有无穷多个2ω-周期解；当时，系统（3.3.1）存在唯一2ω-周期解，且当时，该周期解渐近稳定；当或时不稳定.

证 在定理的条件下，易验证矩阵（3.3.3）为系统（3.3.1）的反射矩阵.当A（t+2ω）=A（t）时，系统（3.3.1）的Poincaré映射为

从而由F（-ω）x=x得（F（-ω）-E）x=0，即

由于该代数方程组的系数行列式为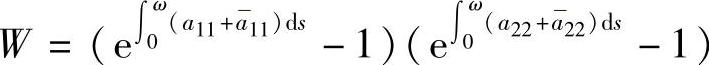：，则应用第2章的引理2.1.1，与第3章定理3.1.3同理可得定理的结论成立.

情形Ⅱ

引理3.3.2 矩阵函数（3.3.4）为反射矩阵，则f₁₁=e^φ11（t），f₂₂=e^φ22（t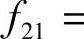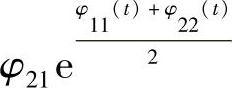），，这里φ₁₁（t），φ₂₂（t），φ₂₁（t）为可微的奇函数.

该引理可与引理3.3.1同理可证.

引理3.3.3[107] 若a₁₂（t）为可微函数，且其零点为孤立点，对∀t有

则线性微分系统（3.3.1）具有形如矩阵（3.3.4）的反射矩阵，当且仅当，

且此时

其中

证 由引理3.3.2得

为系统（3.3.1）的反射矩阵，当且仅当

即

由F（0）=E得，

φ₁₁（0）=φ₂₂（0）=1，φ₂₁（0）=0

又

在式（3.3.7）中将t→-t得

式（3.3.8）+式（3.3.11）得

从而

又由式（3.3.9）得

因此

由此及式（3.3.12）得

再将上式代入式（3.3.10）得

将φ₁₁，φ₂₂，φ₂₁的表达式代入式（3.3.7）即得式（3.3.6），从而引理得证.

定理3.3.2 若引理3.3.3的条件满足，且A（t+2ω）=A（t），则微分系统（3.3.1）的Poincaré映射为T（x）=b（-ω）x.

证 由于A（t+2ω）=A（t），则由引理3.3.3得（3.3.1）的Poincaré映射为

由于a₁₂（t+2ω）=a₁₂（t），则a（t）=a（t+2ω），从而a（ω）=a（-ω）.又a（t）a（-t）=1，故a（ω）a（-ω）=1.因此a（ω）=a（-ω）=1，故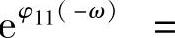

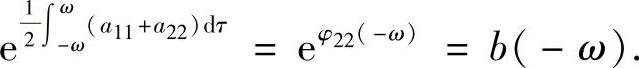
又由于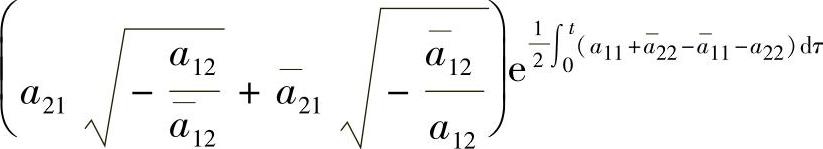为偶的2ω-周期函数，故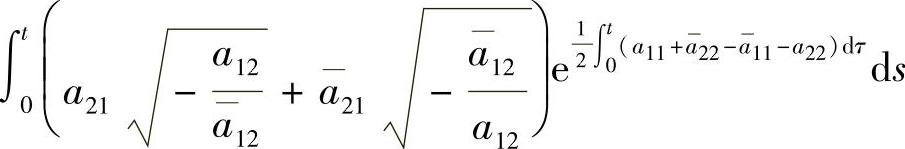为奇的2ω-周期函数，从而有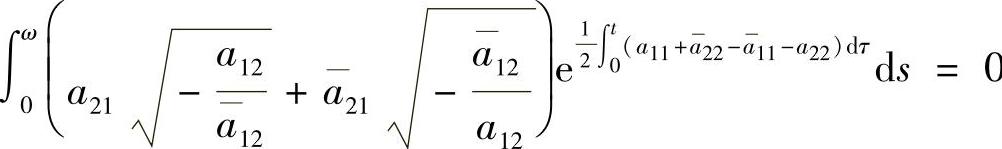.因此φ₂₁（-ω）=0，则

F（-ω）=b（-ω）E.定理得证.

定理3.3.3 在定理3.3.2的条件下，若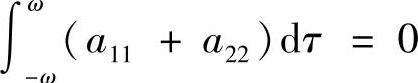，则系统（3.3.1）的一切解皆以2ω为周期.若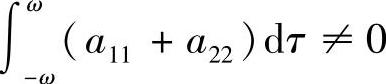，则系统（3.3.1）存在唯一2ω-周期解，且当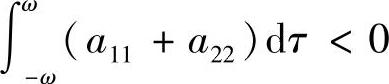时渐近稳定，当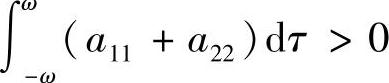时不稳定.

该定理的结论由定理3.3.2，与定理3.2.1同理可证.

例3.3.1 微分系统

这里a，b为任意常数.

当b=3时，该微分系统的解皆为2π-周期；

当b≠3时，该微分系统的唯一周期解为x₁=x₂=0，且当b＜3时，该零解渐近稳定，b＞3时不稳定.事实上，由于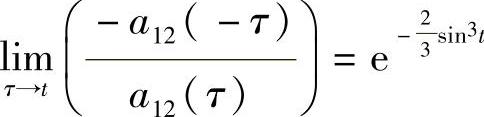.容易验证，该微分系统满足引理

3.3.3的条件，且A（t+2π）=A（t），其反射矩阵F（t）_t=-π=e^2（b-3）πE.由此可得结论成立.

例3.3.2 微分系统

其中a，b，c为任意常数，r（t）为任意连续可微的2π-周期函数.该系统当b=0时，所有解皆为2π-周期解；当b≠0时，存在唯一2π-周期解，并当b＜0时该周期解渐近稳定，当b＞0时不稳定.

由于该微分系统满足引理3.3.3的条件，且F（-π）=e^2bπE.由此即可得上述结论.

例3.3.3 微分系统

其中α，β为常数且α＞1.该微分系统的所有解均为2π-周期.

情形Ⅲ

定理3.3.4[99] 微分系统（3.3.1）以矩阵（3.3.13）为反射矩阵，当且仅当，

其中

证 由反射矩阵的定义得，式（3.3.13）为系统（3.3.1）的反射矩阵，当且仅当，

F′（t）+F（t）A（t）+A（-t）F（t）=0，F（0）=E.

即

由Liouville公式得

所以

从而有

将此代入式（3.3.14）～式（3.3.17）得

又φ（t）+φ（-t）=0.将式（3.3.14）′中的t→-t得式（3.3.14）′与式（3.3.17）′相同.又将式（3.3.15）′中的t→-t得

将此式与式（3.3.16）′相加得(https://www.daowen.com)

将此式代入式（3.3.14）′与式（3.3.15）′得

由cosφ（0）=1，由此及上式得定理的结论成立.

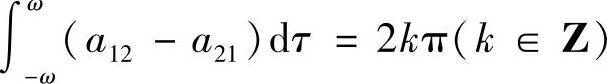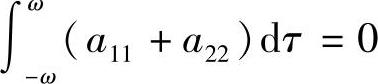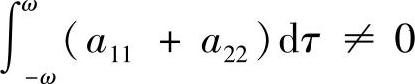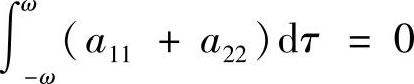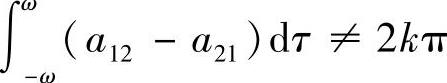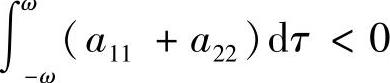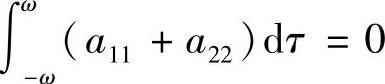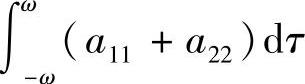
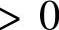推论3.3.1 若定理3.3.4的条件成立，且A（t+2ω）=A（t）.则当和时，微分系统（3.3.1）的所有解皆为2ω-周期解.当或，但，微分系统（3.3.1）存在唯一2ω周期解，且该周期解，当时渐近稳定，时稳定，时不稳定.

证 由A（t+2ω）=A（t），及定理3.3.4知，此时微分系统（3.3.1）的Poincaré映射为

又方程F（-ω）x=x等价于

显然，其系数行列式

W=（α（-ω）-1）2+2α（-ω）（1-cosφ（-ω））.则W=0当且仅当α（-ω）=1和cosφ（-ω）=1，此时系统（3.3.1）的一切解皆为2ω-周期解.当W≠0时，系统（3.2.1）存在唯一2ω-周期解.另一方面，由于F（-ω）x²=α²（-ω）x²，故当α（-ω）＜1，即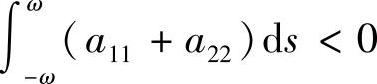时，周期解渐近稳定，时稳定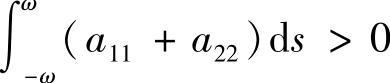，时不稳定^[20].例3.3.4 微分系统

具有反射矩阵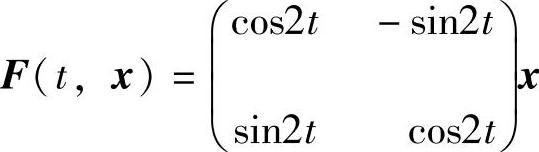，且该系统的一切解皆为2π-周期解.对于n维线性微分系统

A（t）=（a_ij（t））n×n为连续矩阵函数，t∈R.

设F（t，x）=F（t）x为其反射函数.下面将回答何时系统（3.3.19）具有满足关系式

F（t，x）2=α²（t）x². （3.3.20）

的反射函数，其中α（t）为连续可微函数且满足α（0）=α（t）α（-t）=1.^[147]

定理3.3.5 若F（t，x）=F（t）x为系统（3.3.19）的反射函数，则它满足关系式（3.3.20）的充要条件为F（t）F^T（t）=F^T（t）F（t）=α²（t）E（这里E为n×n阶单位矩阵，）.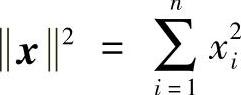

证 设F（t）=（f_ij（t））_n×n，则

当且仅当

即

又

F（t）F^T（t）=F（t）F^T（t）F（t）F^-1（t）=F（t）α²EF（t）=α²E.故定理成立.

定理3.3.6F（t）F^T（t）=α²（t）E，当且仅当，F（t）=α（t）R（t），其中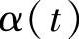

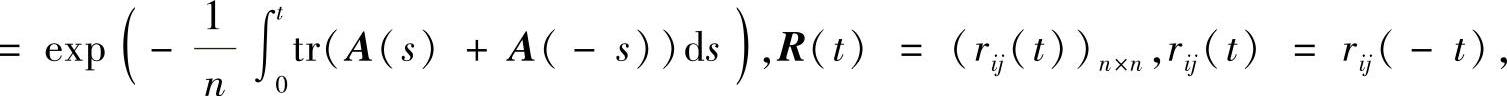
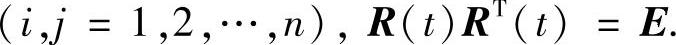
证 由反射矩阵定义知F（t）=X（-t）X^-1（t），这里X（t）为式（3.3.19）的标准基解矩阵，则

从而

即

又由于F（t）F（-t）=E，F（t）F^T（t）=α²（t）E，则F^-1（t）=F（-t）=α^-2F^T（t），取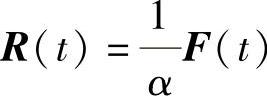，即可推得定理的结论.

定理3.3.7 若F（t）F^T（t）=α²（t）E，并且A（t+2ω）=A（t），则微分系统（3.3.19）的零解，当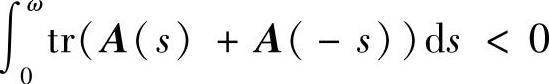时渐近稳定，当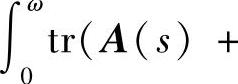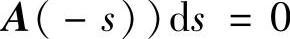时稳定，当∫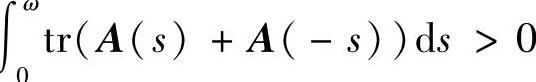时不稳定.

证 由于此时系统（3.3.19）的Poincaré映射T（x）=F（-ω）x满足

T（x）2=F（-ω）x²=α²（-ω）x²，由此推得

Tⁿ（x）2=α²ⁿ（-ω）x² （n=1，2，…） （3.3.21）由此及第1章定义1.2.4可推得定理的结论.

推论3.3.2 若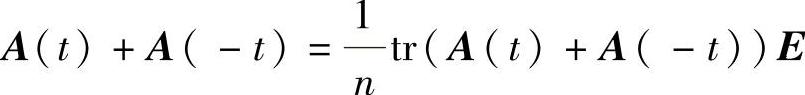，则F（t）F^T（t）=α²（t）E.易验证此时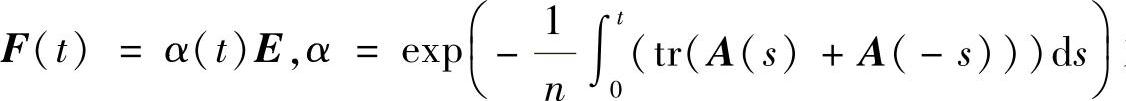为系统（3.3.19）的反射矩阵，显然结论成立.

定理3.3.8 F（t）F^T（t）=α²（t）E的充要条件F（t）B（t）+B（-t）F（t）=0.（3.3.22）这里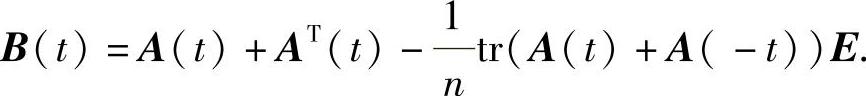

证 令U：=F（t）F^T（t）-α²（t）E，则U（0）=0，

-U′=A（-t）U+UA^T（-t）+（F（t）B（t）+B（-t）F（t））F^T（t），由此式及解的唯一性即可证得定理的结论.

推论3.3.3 若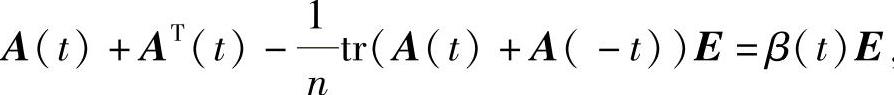，则F（t）F^T（t）=α²（t）E，这里β（t）为任一连续可微的纯量奇函数.

推论3.3.4 若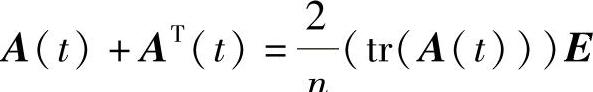，则F（t）F^T（t）=α²（t）E.

由推论3.3.4得：

例3.3.5 微分系统

的反射矩阵F（t），满足F（t）F^T（t）=α²（t）E.这里β（t），γ（t），δ（t）为任意连续可微的2π-周期函数.由于α（-π）=expπ＞1，故该方程的零解不稳定.

定理3.3.9 若F（t）为线性系统（3.3.19）的反射矩阵，并且

则F（t）F^T（t）=α²（t）E，当且仅当，

证 由定理3.1.2知，在条件（3.3.24）成立时，微分系统（3.3.19）的反射矩阵为

由此F（t）F^T（t）=α²（t）E，当且仅当，

将此式关于t求导，并将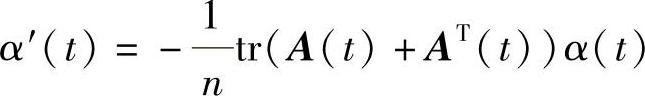代入计算即可得定理的结论成立.

由式（3.3.27）知，当A（t）+A（-t）为对角矩阵或某些特殊矩阵时，我们就可以具体写出F（t）.当A（t）+A（-t）为一般矩阵时，又如何计算F（t）的具体元素呢？

由式（3.3.26）和式（3.3.27）得

其中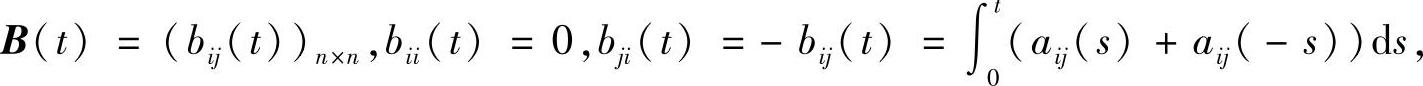

（i≠j，i，j=1，2，…，n）.

下面为了计算F（t），只需计算expB（t）.当n=2时，前面已讨论过了，在此我们考虑n≥3的情形.[147]

定理3.3.10 当n=3时，若条件（3.3.24），条件（3.3.25）及条件（3.3.26）成立，则微分系统（3.3.19）的反射矩阵为

又若A（t+2ω）=A（t），则当δ=0时，微分系统（3.3.19）具有无限多个2ω-周期解；当δ≠0时，它具有唯一的2ω-周期解，且该周期解当δ＜0时渐近稳定，当δ＞0时不稳定.这里

证 由式（3.3.28）计算得

B^2k（t）=（-λ²）^k-1B²（t），B^2k+1（t）=（-λ²）^kB（t），k=1，2，…从而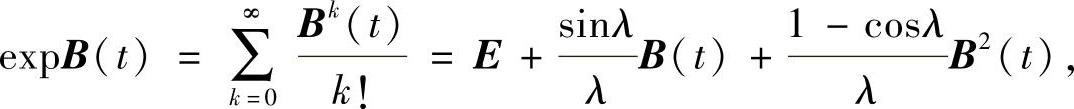即F（t）可由式（3.3.29）表示.

又当系统（3.3.19）为2ω-周期系统时，此时其Poincaré映射T（x）=F（-ω）x，则方程F（-ω）x=x的系数行列式

W=det（F（-ω）-E）=（α（-ω）-1）[（α（-ω）-1）²+2α（-ω）（1-cosλ（-ω））].由此即可推得定理的结论成立.

同理可得

定理3.3.11 当n=4时，若条件（3.3.24），条件（3.3.25）及条件（3.3.26）满足，且b₂₃b₁₄-b₂₄b₁₃+b₃₄b₁₂=0，则微分系统（3.3.19）的反射矩阵可由式（3.3.29）表示.其中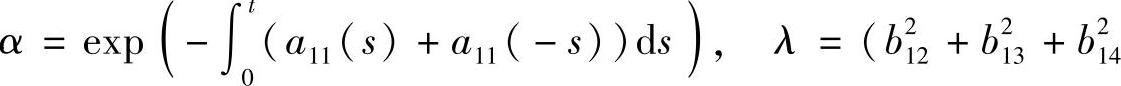

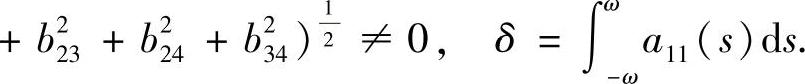
又当A（t+2ω）=A（t）时，与定理3.3.10相应的结论也成立.

注意，此时方程F（-ω）x=x的系数行列式为

W=det（F（-ω）-E）=[α（-ω）-1]²[（α（-ω）-1）²+2α（-ω）（1-cosλ（-ω））].

由定理3.3.10和定理3.3.11可以猜想，对任意的n≥3，在一定条件下，微分系统（3.3.19）以式（3.3.29）为反射矩阵，并且有

W=det（F（-ω）-E）

=[α（-ω）-1]^n-2[（α（-ω）-1）²+2α（-ω）（1-cosλ（-ω））].