考虑线性微分系统

这里P（t）为连续矩阵函数.

设X（t）为式（3.1.1）的基解矩阵，则其通解为φ（t；τ，x）=X（t）X^-1（τ）x，则其反射函数为F（t，x）=φ（-t；t，x）=X（-t）X^-1（t）x.

定义3.1.1 称F（t）=X（-t）X^-1（t）为系统（3.1.1）的反射矩阵.

由反射函数的性质可推得反射矩阵F（t）具有如下性质：

1） F（-t）F（t）≡F（0）=E. （3.1.2）

2） F（t）为系统（3.1.1）的反射矩阵的充要条件为F（t）为Cauchy问题

的解.

由Liouville公式得

3）对任一非奇异且满足式（3.1.2）的矩阵F（t），存在一个线性系统

以F（t）为反射矩阵.

显然F（t）x+x=c为式（3.1.4）的解，从而式（3.1.4）任一解x（t）有x（t）+x（-t）=2x（0）成立.系统（3.1.4）称为以F（t）为反射矩阵的简单线性系统.系统（3.1.1）为简单线性系统的必要条件为P（t）≡P（-t）F（t）.

4）以F（t）为反射矩阵的线性系统均可表示为

这里R（t）为任意连续矩阵函数，t∈R.

定理3.1.1 对于微分系统（3.1.1），P（t）为连续矩阵，对充分小t，存在唯一微分系统

与系统（3.1.1）具有相同的反射矩阵F（t），且Q（t）=Q（-t）.若系统（3.1.1）与系统（3.1.5）皆为2ω-周期系统，则它们具有同一Poincaré映射.

证 设F（t）为系统（3.1.1）的反射矩阵.

下面来求解

F′（t）+F（t）Q（t）+Q（t）F（t）=0. （3.1.6）

由于方程F（t）-λE=0的特征根，当t=0时为1，则对t＜＜1，矩阵F（t）与-F（t）没有公共根，由参考文献[27]得方程（3.1.6）存在唯一解Q（t）.下证Q（t）=Q（-t）.事实上，在式（3.1.6）中令t→-t，则有

F′（-t）+F（-t）Q（-t）+Q（-t）F（-t）=0. （3.1.7）

又F（t）F（-t）=E.则F′（t）F（-t）=F（t）F′（-t）.将式（3.1.7）两端左乘F（t）得

F（t）F′（-t）+F（t）F（-t）Q（-t）+F（t）Q（-t）F（-t）=0，

即

F′（t）F（-t）+Q（-t）+F（t）Q（-t）F（-t）=0.

两边右乘F^-1（-t）得

F′（t）+Q（-t）F^-1（-t）+F（t）Q（-t）=0，

即

F′（t）+Q（-t）F（t）+F（t）Q（-t）=0.(www.daowen.com)

由于方程（3.1.6）的解唯一，从而Q（t）≡Q（-t）.由此及式（3.1.6）知，微分系统（3.1.5）以F（t）为反射矩阵.

定理3.1.2 设P（t）为R上的连续矩阵函数，并满足

则系统（3.1.1）具有反射矩阵

证 显然

F（0）=E，F（t）F（-t）=E.

下面验证F（t）满足式（3.1.3）即可.

事实上，由条件P（t）与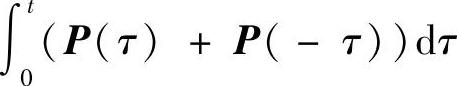可交换，则P（-t）与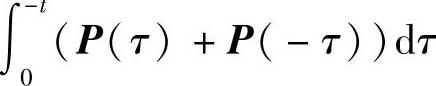也可交换，从而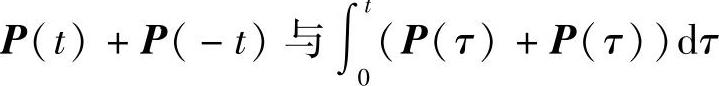可交换，则

F′（t）=-（P（t）+P（-t））F（t），F（t）P（t）=P（t）F（t），从而有

即F（t）为系统（3.1.1）的反射矩阵.（这里P：=P（-t））

定理3.1.3 设P（t+2ω）=P（t），且P（t）在R上连续，并满足关系式（3.1.8），则系统（3.1.1）的Poincaré映射为

并且当特征方程

的所有特征根λ_k，有Reλ_k＜0时，系统（3.1.1）渐近稳定，若存在一个特征根λ_k，有Reλ_k＞0时，该系统不稳定.

证 由定理3.1.2得

又由于

F（t）=X（-t）X^-1（t），

则

F（-ω）=X（ω）X^-1（-ω）=X（-ω）X（2ω）X^-1（-ω），

即F（-ω）相似于X（2ω）.由此即可得定理的结论成立.

注3.1.1 由参考文献[116]知，系统（3.1.1）的反射矩阵可表示为F（t）=e^S（t）x，其中S（t）=ln（X（-t）X^-1（t））且S（-t）+S（t）=0.

定理3.1.4 微分系统（3.1.1）具有形如F（t，x）=e^Atx的反射函数的充要

条件为

-2P（0）exp（-2P（0）t）+exp（-2P（0）t）P（t）+P（-t）exp（-2P（0）t）≡0，且此时F（t，x）=e^-2P（0）tx.

该结论直接由反射函数的定义可证.

推论3.1.1 在定理3.1.4的条件下，若P（t+2ω）=P（t），则微分系统

（3.1.1）的任一解x（t）为2ω-周期解的充要条件为x（-ω）=ζ为代数方程

[e^2P（0）ω-E]ζ=0

的解.若det（e^2P（0）ω-E）≠0，则x=0为系统（3.1.1）的唯一2ω-周期解，且当特征方程2P（0）ω-λE=0的特征根λ_k满足Reλ_k＜0时，渐近稳定.若存在λ_k使得Reλ_k＞0，则该周期解不稳定.

该推论可由定理3.1.3和定理3.1.4直接推得.