考虑微分系统

这里X（t，x）连续可微，其Cauchy问题的解存在唯一.

定义2.3.1 若微分系统

与微分系统（2.3.1）具有相同的反射函数，则称它们是等价的.具有相同反射函数的微分系统称为同一等价类.

由2.2节定理2.2.2知，以F（t，x）为反射函数的微分系统具有形式

这里R（t，x）为任意连续可微函数，其右端连续可微.所有具有形如式（2.3.3）的系统都属于同一等价类.

若取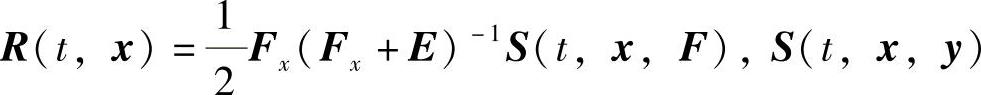为任意连续可微函数且满足S（-t，y，x）+S（t，x，y）=0，则式（2.3.3）具有形式

若取S（t，x，y）=X（t，x）-X（-t，y），则S（t，x，y）+S（-t，y，x）=X（t，x）-X（-t，y）+X（-t，y）-X（t，x）=0.由定义2.3.1知，微分系统（2.3.1）和系统（2.3.2）属于同一等价类的充要条件为存在连续可微函数F（t，x）满足

例2.3.1 考察微分方程

与

是否属于同一等价类？

只要考虑式（2.3.5）有没有解，即方程组

有没有解？将以上前两式相减得2F_xsint-2sint=0，即F_x=1，从而得F_t=-x²-F²，F_tx=-2x-2FF_x=-2x-2F.又F_xt=0，则F=-x，与F（0，x）=x矛盾.故方程①与方程②不属于同一等价类.

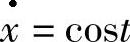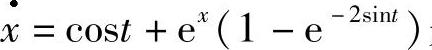若系统（2.3.1）与系统（2.3.2）中有一个可积，那要判定它们是否等价，就容易些了.例2.3.2 方程与是等价的，它们的反射函数为F=x-2sint.

若微分系统（2.3.1）和系统（2.3.2）属于同一等价类，并且系统（2.3.1）为2ω-周期系统，则若系统（2.3.1）和系统（2.3.2）的解在[-ω，ω]上有定义，且分别为φ（t；-ω，x），ψ（t；-ω，x），则系统（2.3.1）的Poincaré映射为T（x）=φ（ω；-ω，x）=F（-ω，x）=ψ（ω；-ω，x），由此可推得

定理2.3.1 若微分系统（2.3.1）为2ω-周期系统，且它与微分系统（2.3.2）属于同一等价类，它们的解在[-ω，ω]上存在，则系统（2.3.1）的2ω-周期解与系统（2.3.2）满足x（-ω）=x（ω）的解一一对应.

例2.3.3 方程

与方程

属于同一等价类，它们的反射函数为F（t，x）=xe^-2t.由F（-π，x）=x，得x=0，故方程①有唯一2π-周期解x=0，从而方程②满足x（π）=x（-π）的解唯一.

推论2.3.1 若微分系统（2.3.1）为2ω-周期系统，它与系统（2.3.2）属于同一等价类，且它们的解在[-ω，ω]上存在，则微分系统（2.3.2）的2ω-周期解ψ（t；-ω，x）与系统（2.3.1）的2ω-周期解φ（t；-ω，x）相对应.

证 由于ψ（t+2ω；-ω，x）=ψ（t；-ω，x），则

ψ（ω；-ω，x）=ψ（t+2ω；-ω，x）t=-ω=ψ（t；-ω，x）t=-ω=x.

故

F（-ω，x）=ψ（ω；-ω，x）=x，

即

由定理2.3.1得它与系统（2.3.1）的2ω-周期解一一对应.

引理2.3.1 若微分系统（2.3.1）的解在R上存在，则与其属于同一等价类的微分系统可以写成下面形式

这里F为系统（2.3.1）的反射函数，R为任意连续可微函数，且保证式（2.3.6）的右端关于x连续可微.

证 设系统（2.3.2）与系统（2.3.1）属于同一等价类，由前面的讨论知，任何以F为反射函数的微分系统均可表示成式（2.3.3）的形式，即

X（t，x）=-（F_x+E）^-1F_t+F_x^-1R₁（t，x）-R₁（-t，F），

Y（t，x）=-（F_x+E）^-1F_t+F_x^-1R₂（t，x）-R₂（-t，F）.

由此得

Y（t，x）=X（t，x）-F_x^-1R（t，x）-R（-t，F），

这里R=R₂-R₁，即任何与系统（2.3.1）等价的微分系统（2.3.2）可表示成式（2.3.6）的形式.

下面验证，具有式（2.3.6）形式的微分系统以F为反射函数.

事实上，由于

F_t+F_xX（t，x）-X（-t，F）=0，

则

F_t+F_x[X+F_x^-1R-R（-t，F）]+X（-t，F）+

F_x^-1（-t，F）R（-t，F）-R（t，x）

=R-F_xR（-t，F）+F_xR（-t，F）-R=0.(www.daowen.com)

从而式（2.3.6）以F为反射函数，即它与系统（2.3.1）属于同一等价类.

定理2.3.2 若微分系统（2.3.1）与某一自治系统等价，则该自治系统为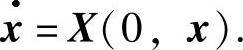

证 设F（t，x）为系统（2.3.1）的反射函数，且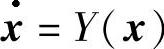与系统(2.3.1)等价，则由引理2.3.1得

Y（x）=X（t，x）+F_x^-1R（t，x）-R（-t,F)

令t=0得

Y（x）=X（0，x）+R（0，x）-R（0，x）=X(0,x).与自治系统等价的非自治系统将在第7章进行详细介绍.

推论2.3.2 设P（t）为连续矩阵函数，线性微分系统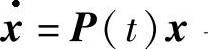与某个自治系统等价，当且仅当

P（-t）+e^-2tP（0）P（t）e^2tP（0）≡2P（0）.

若P（t+2ω）=P（t），则该等价于自治系统的周期系统的Poincaré映射为T（x）=e^2ωP（0）x.

证 由定理2.3.2知，对于线性系统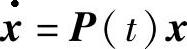，若它与某个自治系统等价，则该自治系统为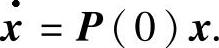又易验证该自治系统的反射函数为F（t，x）=e^-2tP（0）x.则它也是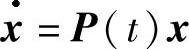的反射函数，故由反射函数的定义知F=e^-2tP（0）x满足推论的条件.

定义2.3.2 称微分系统

为以F（t，x）为反射函数的最简单系统.

显然

F（t，x）+x=C （2.3.8）

为系统（2.3.7）的解.若x（t）为系统（2.3.7）的任一解，且x（0）有意义，则F（t，x（t））=x（-t），从而有x（-t）+x（t）=C=2x（0），两边关于t求导得f（t，x（t））-f（-t，x（-t））=0，即f（t，x）=f（-t，F（t，x））.

定理2.3.3 若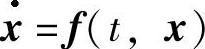为最简单系统，且以F为反射函数，则f（t，x）=f（-t，F（t，x））.

证 由于f（t，x）=-（F_x+E）^-1F_t，则

f（-t，F（t，x））=-（F_x（-t，F（t，x））+E）^-1F_t（-t，F）

=-（F_x^-1+E）^-1F_x^-1F_t=-（F_x+E）-1F_t=f（t，x）.

由该定理知一个系统是否为最简单系统，首先要看其是否存在可微函数F（t，x）满足f（t，x）=f（-t，F（t，x））.

例2.3.4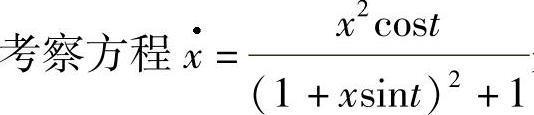是否为最简单方程？

解 若它为简单方程，则方程f（t，x）=f（-t，F）有解，即

即

（F+x）[F-x+xFsint]=0，

由此推得

又F为反射函数，F（0，x）=x，故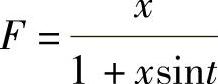，且

经计算可得，该式成立，从而所观察的微分方程为最简单方程.又由于F（-π，x）=x，故该微分方程在[-π，π]上有意义的一切解皆为2π-周期解.

例2.3.5 考察微分方程 x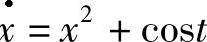是否为最简单方程？

解 先看方程x²+cost=F²+cost有没有解.显然F=±x为其解，又F（0，x）=x，则F=x，又F_t+F_x（x²+cost）+F²+cost≠0，故F=x不是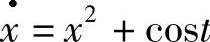的反射函数，从而它不是最简单方程.

定义2.3.3 称微分系统

为以F（t，x）为反射函数的简单系统.

引理2.3.2 微分系统（2.3.1）为简单系统，当且仅当，对其反射函数F（t，x）成立

F_x（t，x）X（t，x）=X（-t，F（t，x））. （2.3.10）

证 必要性 设微分系统（2.3.1）为以F（t，x）为反射函数的简单系统，则

F_t+F_xX（t，x）+X（-t，F）=0，F（0，x）=x， （2.3.11）

将式（2.3.12）代入式（2.3.11）可得必要性成立.

充分性 若式（2.3.10）成立，且F（t，x）为其反射函数，则式（2.3.11）成立，将式（2.3.10）代入式（2.3.11）即可推得式（2.3.12）成立，从而系统（2.3.1）为以F（t，x）为反射函数的简单系统.

定理2.3.4 若X（t，x）=X（x），则系统（2.3.1）为简单微分系统.

证 由参考文献[46]知，微分系统（2.3.1）过（t₀，x₀）的解为x=φ（t-t₀；0，x₀），则其反射函数为F（t，x）=φ（-2t；0，x），从而有F_t=-2φ′_t（-2t；0，x）=-2X（φ（-2t；0，x））=-2X（F），又由式（2.3.11）可推得F_xX（x）=X（F），由引理2.3.2可得定理的结论成立.