反射函数在微分系统中的理论与应用

设F（t，x）：D→Rⁿ，D⊂Rⁿ⁺¹，0∈D.F（t，x）在D上连续可微且满足

F（-t，F（t，x））≡x， （2.2.1）

F（0，x）≡x. （2.2.2）

引理2.2.1 若连续可微函数F（t，x）满足式（2.2.1）和式（2.2.2），则有

F_x（-t，F（t，x））≡F_x^-1（t，x）； （2.2.3）

F_t（-t，F（t，x））≡F_x^-1（t，x）F_t（t，x）. （2.2.4）

证 将式（2.2.1）两边关于t和x求偏导数得

F_x（-t，F（t，x））F_x（t，x）≡E，

-F_t（-t，F（t，x））+F_x（-t，F（t，x））F_t（t，x）≡0，

由此即可推得引理成立.这里E-为n×n阶单位矩阵.

定理2.2.1 对于二阶连续可微函数F（t，x）满足式（2.2.1）和式（2.2.2），对于∀x∈Rⁿ，充分小的t，存在微分系统

以F（t，x）为反射函数，其首次积分为

F（t，x）+x=C=常数. （2.2.6）

证 由F_x（0，x）=E，则F_x（t，x）+E在t=0时，其特征值λ_i（0，x）=2，因此对∀x∈Rⁿ和充分小的t，F_x（t，x）+E为可逆矩阵，则微分系统（2.2.5）存在.

下面验证F（t，x）确是系统（2.2.5）的反射函数.

事实上，由引理2.2.1得

F_t+F_xX（t，x）+X（-t，F）

=F_t-F_x（F_x+E）^-1F_t-（F_x（-t，F）+E）^-1F_t（-t，F）

=F_t-F_x（F_x+E）^-1F_t-（F_x^-1+E）^-1F_x^-1Ft

=F_t-F_x（F_x+E）^-1F_t-（F_x（F_x^-1+E））^-1F_t

=F_t-F_x（F_x+E）^-1F_t-（E+F_x）^-1F_t

=F_t-（F_x+E）（E+F_x）^-1F_t=0.

故F（t，x）为系统（2.2.5）的反射函数.

又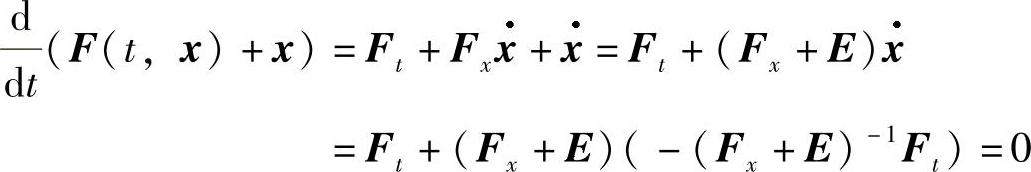

故F（t，x）+x=C为系统（2.2.5）的首次积分.

推论2.2.1 二次连续可微函数F（t，x）：D→R为某个微分系统的反射函数，当且仅当，F（t，x）满足式（2.2.1）和式（2.2.2）.

证 显然，由定理2.2.1得充分性成立.必要性由反射函数的性质2可由本章的式（2.1.4）直接推得.

定理2.2.2 若Φ：G→Rⁿ为某个连续可微的微分系统的反射函数，二次连续可微函数F：D→Rⁿ满足式（2.2.1）和式（2.2.2）.则在G∩D上F≡Φ的充要条件为该微分系统具有形式

这里R：D∩G→Rⁿ上的任一连续可微的向量函数.

证 必要性 设Φ为微分系统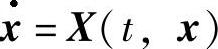的反射函数，且Φ≡F.(https://www.daowen.com)

令

则由式（2.2.3）和式（2.2.4）及基本关系式（2.1.5）得

充分性 设R连续可微，下面验证F为系统（2.2.7）的反射函数.事实上，由式（2.2.3）和式（2.2.4）得

F_t+F_xX（t，x）+X（-t，F）

=F_t+F_x[-（F_x+E）^-1F_t+F_x^-1R（t，x）-R（-t，F）]-（F_x（-t，F）+E）^-1F_t（-t，F）+F_x^-1（-t，F）R（-t，F）-R（t，x）

=F_t-F_x（F_x+E）^-1F_t-（F_x+E）^-1F_t

=F_t-（F_x+E）（F_x+E）^-1F_t=0.

由此得充分性成立.

例2.2.1 形如

的微分方程具有反射函数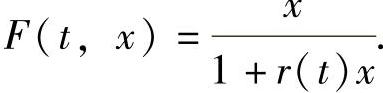这里r（t）为任意可微的奇函数，R（t，x）为任意连续可微函数.

综上可得，对于任意一个二次可微函数F（t，x）满足式（2.2.1）和式（2.2.2），我们总可以建立一个微分系统族（2.2.7）以F（t，x）为反射函数，那么我们就可以利用反射函数的性质来研究微分系统族解的性态，在后面的章节里我们将详细介绍.

当F（t，x）为一个隐函数时，我们也可适当选取R（t，x）使系统（2.2.7）为一个不显含F（t，x）的微分系统.

譬如，F（t，x）由隐式方程

U（-t，F）=U（t，x） （2.2.8）

给出，这里U为可微函数，且detU_x≠0.

建立微分方程系统

易验证U（t，x）=C为式（2.2.9）的解，因此对式（2.2.9）的任一解x（t）有U（-t，x（-t））=U（t，x（t）），由此得式（2.2.9）的反射函数可由式（2.2.8）给出.

由式（2.2.8）得

F_x=U_x^-1（-t，F）U_x；F_x^-1=U_x^-1U_x（-t，F），

易验证F（t，x）为系统

的反射函数.

若取R（t，x）=U_x^-1（-t，F（t，x））S（t，U（t，x）），则

R（-t，F）=U_x^-1S（-t，U（-t，F））=U_x^-1S（-t，U），

从而式（2.2.10）可改写成

由上看出式（2.2.11）右端已经不含F，由此可证

定理2.2.3 对于任意连续可微函数S（t，x），U（t，x）且detU_x≠0，微分系统

的反射函数由关系式U（-t，F）=U（t，x）确定.

例2.2.2 微分方程

的反射函数由关系式2F+sinF=2x+sinx+2sint确定，并且当S为t的2π-周期函数时，该微分方程在[-π，π]上有定义的解皆为2π-周期解，因为F（-π，x）≡x.