考虑微分系统

假设X（t，x）有连续的偏导数，其Cauchy问题的解存在唯一，记为φ（t；τ，x），I_x为解φ（t；0，x）的存在区间.

记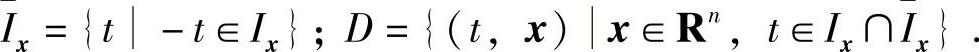

定义2.1.1 称可微函数

F（t，x）△=φ（-t；t，x），（t，x）∈D （2.1.2）

或者F（t，x）=φ（-t，t）（x）=φ（-t；0，φ（0；t，x））为微分系统（2.1.1）的反射函数.

反射函数具有下列性质：

1）对微分系统（2.1.1）的任一解x（t），t∈I，t₀∈I有

F（t，x（t））≡x（-t）； （2.1.3）

2）对任一反射函数F有恒等式

F（-t；F（t，x））≡F（0，x）≡x； （2.1.4）

3）可微函数F：D→Rⁿ为微分系统（2.1.1）的反射函数，当且仅当，它为偏微分方程

的解.我们称式（2.1.5）为关于反射函数的基本关系式.

证 1）设x（t）为式（2.1.1）的任一解，则x（t）=φ（t；t₀，x₀），从而F（t，x（t））=φ（-t；t，φ（t；t₀，x₀））=φ（-t；t₀，x₀）=x（-t）.

2）由1）得F（-t，F（t，x（t）））=F（-t，x（-t））=x（t），即F（-t，F（t，x））=x.又F（0，x）=φ（-t；t，x）_t=0=φ（0；0，x）=x.则式（2.1.4）成立.

3）必要性 由1）得，对式（2.1.1）任一解x（t）有F（t，x（t））=x（-t），两边关于t求导得

由此可得

F_t+F_xX（t，x）+X（-t，x（-t））=0，

即 F_t+F_xX（t，x）+X（-t，F（t，x））=0.

又由2）得F（0，x）=x，从而式（2.1.5）和式（2.1.6）成立.

充分性 若Φ为式（2.1.5）和式（2.1.6）的解，又因为微分系统（2.1.1）的反射函数F也满足式（2.1.5）和式（2.1.6），则由偏微分方程Cauchy问题解的唯一性得Φ≡F，即Φ为系统（2.1.1）的反射函数.

引理2.1.1 （基本引理） 若X（t+2ω，x）=X（t，x），则该微分系统（2.1.1）的Poincaré映射T（x）可以定义为T（x）=F（-ω，x）=φ（ω；-ω，x），从而系统（2.1.1）的解φ（t；-ω，x）为2ω-周期解，当且仅当x为方程

F（-ω，x）=x （2.1.7）

的解.

该引理的结论可由第1章定理1.2.1取α=-ω推得.

定理2.1.1 若X（t+2ω，x）=X（t，x），且X（-t，x）+X（t，x）≡0，则微分系统（2.1.1）在[-ω，ω]上有定义的解皆为2ω-周期解且是t的偶函数.

证 显然，在定理的条件下，F（t，x）=x为系统（2.1.1）的反射函数，又F（-ω，x）≡x，F（t，x（t））=x（-t）=x（t），故由引理2.1.1得定理的结论成立.

由引理2.1.1知，我们可以通过寻找2ω-周期系统的反射函数，来建立其Poincaré映射，从而其周期解的存在性和稳定性问题就迎刃而解了.那么，很自然要问，如何来寻找其反射函数呢？特别是对于不可积系统，我们能否找到其反射函数？关于这些问题的回答，我们将在后面章节中详细介绍.

先看一个简单的例子，若系统（2.1.1）为不可积系统，且X（0，x）=0，建立微分系统

该系统右端函数为t的奇函数，且该系统为不可积系统，由定理2.1.1知，该系统的反射函数为F（t，x）=x.

又例如Riccati方程：x=（x²+cos²t）sint为不可积的，而其反射函数也是F（t，x）≡x.由此可知，对于不可积系统我们也能找到其反射函数.

下面我们来阐述反射函数与周期解之间的关系.(www.daowen.com)

定理2.1.2 若微分系统（2.1.1）的所有解均为2ω-周期解，则该系统的反射函数F（t，x）也是t的2ω-周期函数.

证 设φ（t；τ，x）为微分系统（2.1.1）的通解表达式，且有φ（t+2ω；τ，x）=φ（t；τ，x），则

φ_{（t，t+2ω）}（x）=φ（t；t+2ω，x）=φ（t+2ω；t+2ω，x）=x，

从而有

F（t+2ω，x）=φ（-t-2ω；t+2ω，x）=φ（-t；t+2ω，x）

=φ_{（-t，t+2ω）}（x）=φ_（-t，t）°φ_{（t，t+2ω）}（x）

=φ_（-t，t）（x）=φ（-t；t，x）=F（t，x）.

即F是关于t的2ω-周期函数.

定理2.1.3 若微分系统（2.1.1）是关于t的2ω-周期系统，而且其所有解都在[-ω，ω]上存在.若系统（2.1.1）的反射函数F（t，x）为t的2ω-周期函数，则系统（2.1.1）的所有解是t的4ω-周期函数.

证 由于X（t+2ω，x）=X（t，x），则X（t+4ω，x）=X（t，x）.又

F（t+2ω，x）=F（t，x），

取t=-2ω得

F（0，x）=F（-2ω，x）≡x，

则由引理2.1.1知φ（t；-2ω，x）为4ω-周期解.

注2.1.1 在定理2.1.3的条件下，若F（t+ω，x）=F（t，x），则系统（2.1.1）的解为2ω-周期解.若F（t+2ω，x）=F（t，x），一般情况下不能推出系统（2.1.1）的解为2ω-周期解.

例2.1.1 微分系统

为2π-周期系统，其解

为4π-周期函数.但其反射函数

为2π-周期函数.

但也不是对于所有2ω-周期系统，若其解均是2ω-周期函数，就能推出其反射函数为ω-周期函数.

例2.1.2 微分方程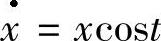为2π-周期方程，其通解为x=x₀e^sint-sint0为2π-周期函数，但其反射函数F=xe^-2sint不是π-周期函数.

对于微分方程（即n=1）时，我们有下面的结论成立.

定理2.1.4 若微分方程（2.1.1）为2ω-周期的，而且其解在t∈[-ω，ω]上存在，则方程（2.1.1）的所有解均为2ω-周期函数，当且仅当，其反射函数F（t，x）为t的2ω-周期函数.

证 必要性由定理2.1.2直接可得.

下证充分性 反证 若存在一个解x（t），它不是2ω-周期函数，则x（2kω），k∈N，为严格单调点列[17]，从而x（t）也不可能为4ω-周期函数，这与定理2.1.3矛盾，因此充分性成立.

由定理2.1.3、定理2.1.4可以看出，对2ω-周期系统在R上有定义的所有解为周期函数的充要条件为其反射函数为t的ω的倍周期函数.

例2.1.3 微分系统

a（t），b（t），c（t）为2ω-周期函数，且b（t）+b（-t）=0，c（t）+c（-t）=0.可以验证其反射函数为

则其Poincaré映射

由此可得，当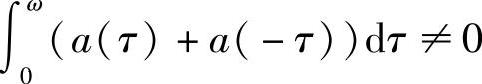时，T（x，y）=（x，y）T有唯一解（x，y）=（0，0），即此时微分系统（2.1.8）有唯一2ω-周期解x=0，y=0.并且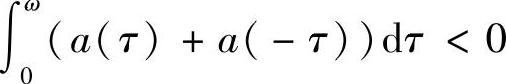，当时稳定，当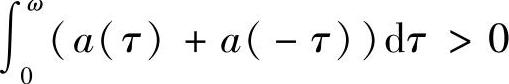时不稳定.当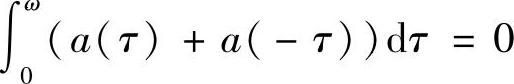时，系统（2.1.8）的所有解均为2ω-周期解.

由上例看出，利用反射函数来研究微分系统周期解的存在性和稳定性，是很方便实用的.为了充分利用反射函数的性质来研究解的性态，下面我们来研究哪些微分系统以已知函数为反射函数.