考虑Cauchy问题:
其中x为Rn中的向量,f是实变量t和n维向量x的n维向量值函数.
定理1.1.1 (存在唯一性定理)
若f(t,x)在开区域G⊆R×Rn中满足下列条件:
1)f在G内连续,简记为f∈C(G);
2)f关于x满足局部Lipschitz条件,即对于点P0(t0,x0)∈G,∃ G0={(t,x)|t-t0|≤a,x-x0≤b}⊂G
和依赖于P0点的常数Lp0,使得对∀(t,x1),(t,x2)∈G0,有不等式 f(t,x1)-f(t,x2)≤Lp0x1-x2 (1.1.2)
成立,其中·表示欧氏范数.
则Cauchy问题(1.1.1)在区间t-t0≤h∗上存在唯一的解,其中
证 容易看出,在区间t-t0≤h∗上Cauchy问题(1.1.1)等价于积分方程
的求解问题.取B为定义在区间t-t0≤h∗上的一切连续函数所构成的空间,D为定义在区间t-t0≤h∗上且图像包含在G0中的一切连续函数所构成的集合.现定义在连续函数空间C[t0-h∗,t0+h∗]上的映射:
由于
所以,映射(1.1.5)把集合D映射到它自身.要证明积分方程(1.1.4)存在唯一解,也就是要证明映射(1.1.5)存在唯一的不动点:x∗=Tx∗.下面利用Banach空间的压缩映像原理来证明.
设∀x1,x2∈D,由式(1.1.4)得
由Lipschitz条件(1.1.2)知
由式(1.1.3)知,Lp0h∗<1.因此,由式(1.1.5)所定义的映射T是一压缩映射,由压缩映射原理知其存在唯一的不动点.(这里以及下文中的范数都为欧氏范数)
由定理1.1.1知道,Cauchy问题(1.1.1)的解,至少在t-t0≤h∗上存在,这一局部性的存在定理大大限制了解的实用范围和理论研究,人们自然要问,对于给定的Cauchy问题,能否确定其解存在唯一的最大区间?下面将给予肯定的回答.
假设定理1.1.1的条件成立,由定理1.1.1可知,Cauchy问题(1.1.1)的解在区间t-t0≤h∗上存在唯一.我们先将解向右延拓,令t1=t0+h∗,x(t0+h∗)=x1,易见若P1(t0+h∗,x(t0+h∗))∈G0⊂G,由于P1是G的内点,故必存在闭区域
G1={(t,x)t-t1≤a1, x-x1≤b1}⊂G,
使f在G1上对x满足Lipschitz条件,从而再根据定理1.1.1,此方程过点P1的解记作x1(t),它必在区间t-t0≤h1∗上存在唯一,其中h1∗可类似于式(1.1.3)的定义.根据解的唯一性可知,在区间[t1-h1∗,t1]上,此方程过P1的解x1(t)必与过P0的解x0(t)重合.
定义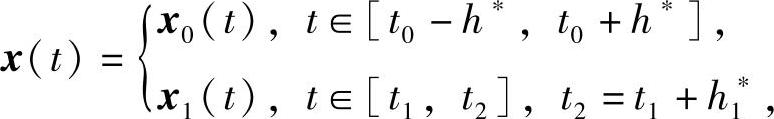
于是x(t)就是Cauchy问题(1.1.1)在区间[t0-h∗,t2]上的唯一解.
若P2(t2,x(t2))是G的内点,则可依上法再向右延拓.同理,可将解从点(t0-h∗,x(t0-h∗))向左延拓.如此继续,直到双方都不能再延拓为止.这时所得到的存在区间,称为解的最大存在区间,具有最大存在区间的解称为饱和解.容易看出,此最大存在区间必为开区间,记作(α,β),因为若一方(例如t=β)为闭,则解必可从t=β向右继续延拓.
定理1.1.2 设f(t,x)在区域G⊆R×Rn内连续有界,且对x满足局部Lipschitz条件,若Cauchy问题(1.1.1)的解x(t)的最大存在区间为(α,β),α,β为有限数,则:
1)极限 ,
,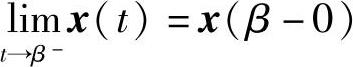 存在;
存在;
2)点(α,x(α+0))与(β,x(β-0))均在G的边界上.
证 1)由于Cauchy问题(1.1)等价于积分方程
从而
其中M为f(t,x)的上界.
由于β为有限数,则当t1,t2→β-时,有x1(t)-x2(t)→0.由Cauchy收敛准则知极限x(β-0)存在.同理可证x(α+0)存在.
2)若(β,x(β-0))不在G的边界上,则必为G的内点.从而可以由t=β-0向右继续延拓,这与(α,β)为解的最大存在区间相矛盾,则证明点(α,x(α+0))与(β,x(β-0))均在G的边界上.
若去掉f有界的条件,则可得如下定理:
定理1.1.3 设f(t,x)∈C(G),且对x满足局部Lipschitz条件,则Cauchy
问题(1.1.1)的解可延拓到G的边界任意接近处(包括可能趋于无穷).
证 作有界区域Gn(n=1,2,…),使(t0,x0)∈G1⊂G2⊂…⊂Gn⊂…⊂G,且G⊂Gn+1(n=1,2,…),Gn→G,当n→+∞时.
对于闭区域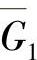 ,f在
,f在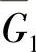 上有界,利用定理1.1.2可知,Cauchy问题(1.1.1)的解可向右延拓至G1的某一边界点P1,P1∈G2.对闭区域G2利用定理1.1.2可知,此解可继续由P1向右延拓至G2的某一边界点P2.依此类推,可得到点列{Pn},n=1,2,….由于当n→+∞时Gn→G,故{Pn}必可与G的边界任意接近.同理可讨论向左延拓.
上有界,利用定理1.1.2可知,Cauchy问题(1.1.1)的解可向右延拓至G1的某一边界点P1,P1∈G2.对闭区域G2利用定理1.1.2可知,此解可继续由P1向右延拓至G2的某一边界点P2.依此类推,可得到点列{Pn},n=1,2,….由于当n→+∞时Gn→G,故{Pn}必可与G的边界任意接近.同理可讨论向左延拓.
定理1.1.4 设f(t,x)在全空间R×Rn上连续、有界,且对x满足局部Lipschitz条件,则Cauchy问题(1.1.1)解的存在区间为(-∞,+∞).
证 由定理1.1.3可知,解可延拓到与R×Rn的边界任意接近,即可延伸至无穷.故要保证可关于t无限延拓,只需证明在定理的条件下,其解在任意有限区间上均有界.事实上,由于
这一结论是显然的.
在定理1.1.4中,要求f在全空间上有界,但这一条件太强,为了减弱条件,下面给出一个著名的引理.
Gronwall引理 设一元函数g(t)与φ(t)在区间[t0,t1]上连续,g(t)≥0,常数λ≥0,r≥0.若
则
证 令
两边对t求导得
ψ′(t)=g(t)φ(t)+r, (1.1.9)(www.daowen.com)
由式(1.1.6)得φ(t)≤ψ(t),代入式(1.1.9)得
ψ′(t)-g(t)ψ(t)≤r,
两端乘以积分因子 得
得
即
两端分别由t0到t积分得
又ψ(t0)=λ,从而有
定理1.1.5 设f(t,x)在全空间R×Rn上连续,对x满足局部Lipschitz条件,且
f(t,x)≤Nx (N为一正常数),
则∀(t0,x0)∈R×Rn,Cauchy问题(1.1.1)的解的存在区间均为(-∞,+∞).
证 仿照定理1.1.4,我们只需证明在任一有限区间上,Cauchy问题(1.1.1)的解都是有界的.假设存在有限数b>t0,使得解x(t)在[t0,b)上无界,当t∈[t0,b)时,有
应用Gronwall引理得
与x(t)在[t0,b)上无界矛盾.所以解向右对t可延拓至+∞.同理可证向左延拓至-∞.
若f的定义域不是全空间而是G=R×D,D⊂Rn,那么定理1.1.4和定理1.1.5均不能保证解关于t可无限延拓,因为解可能在有限时刻到达D的边界,这时有下面定理.
定理1.1.6 设f(t,x)在区域G=R×D,D⊂Rn内连续,有界且满足局部Lipschitz条件,若Cauchy问题(1.1.1)的解的几何长度无限,则此解的存在区间必为(-∞,+∞).
证 设S(t)是解所表示的曲线的弧长函数,S(t0)=0,由弧微分公式可知
其中M是f(t,x)的上界,两端分别从t0到t(t>t0)积分得S(t)≤M(t-t0).由于S(t)无限,所以必有t→+∞.同理可证t→-∞.
定理1.1.7 (解对初值的连续依赖性)
设f(t,x)在域G⊆R×Rn内连续,满足局部Lipschitz条件,(t0,x0)∈G.并设有界闭区间[a,b]为Cauchy问题(1.1.1)的解的一个存在区间,则其解x(t;t0,x0)在区间[a,b]上是初值(t0,x0)的连续函数.
证 为了证明的需要,首先我们来构造一个解曲线段C={x=x(t;t0,x0)a≤t≤b}的邻域U∈G,使得对∀(t,x1),(t,x2)∈U,f对x的Lipschitz条件满足且有共同的Lipschitz常数L.事实上,对于曲线C上任一点Pi必存在一个n+1维空间的球形邻域 ,使得在Ui内f对x的局部Lipschitz条件成立,其Lipschitz常数记作Lpi.由于C是一有界闭集,由有限覆盖定理可知,存在有限个球形邻域Ui(i=1,2,…,m)将曲线C覆盖.取
,使得在Ui内f对x的局部Lipschitz条件成立,其Lipschitz常数记作Lpi.由于C是一有界闭集,由有限覆盖定理可知,存在有限个球形邻域Ui(i=1,2,…,m)将曲线C覆盖.取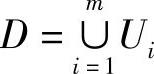 ,且
,且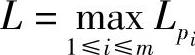 ,容易看出
,容易看出 ,且∀(t,x1),(t,x2)∈D,
,且∀(t,x1),(t,x2)∈D,
f(t,x1)-f(t,x2)≤Lx1-x2 (1.1.10)
成立.设D的边界集合与集合C的距离为d,则以C上每点为中心,d为半径的所有n+1维开球域的全体所构成的区域D0⊆D.
下证解对初值的连续性.设过初始点(t0,x0)与 的解分别为x=x(t;t0,x0)与
的解分别为x=x(t;t0,x0)与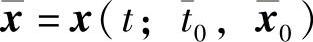 ,即要证对∀ε>0(不妨设ε<d),∃δ(ε)>0,使得只要
,即要证对∀ε>0(不妨设ε<d),∃δ(ε)>0,使得只要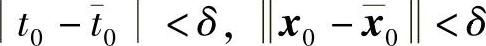 解
解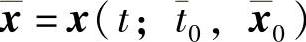 必在区间[a,b]上存在,而且有
必在区间[a,b]上存在,而且有
成立.易见两个解x和x都位于区域D0时有
其中 (或
(或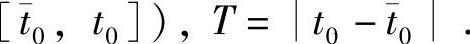
由Gronwall引理得
由式(1.1.12)不难看出,只要选取
则当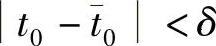 ,
,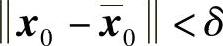 时,过初始点
时,过初始点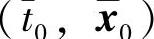 的解
的解 必满足不等式
必满足不等式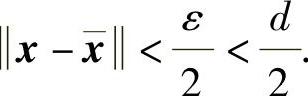 由此可知,解
由此可知,解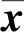 也必在[a,b]上存在.如果x仅在区间
也必在[a,b]上存在.如果x仅在区间 上存在,
上存在,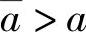 ,
, ,则在区间
,则在区间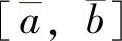 上重复式(1.1.12)导出的过程可得
上重复式(1.1.12)导出的过程可得
从而可知解曲线x(t;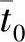 ,
,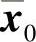 )上的点,(
)上的点,( ;x(
;x(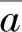 ;
;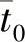 ,
,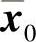 ))与(
))与(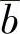 ;x(
;x( ;
; ,
,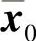 ))均必位于D0内部,从而还可以进一步延拓.
))均必位于D0内部,从而还可以进一步延拓.
于是,当式(1.1.13)成立时,即有式(1.1.11)在区间[a,b]上成立.
定理1.1.8 (解对方程右端函数的连续依赖性)
设f(t,x)满足定理1.1.7的条件,则在区间[a,b]上,Cauchy问题(1.1.1)的解将随方程的右端函数f(t,x)而连续变化.
证 考察Cauchy问题:
其中f与g在G⊆R×Rn上连续,且均满足局部Lipschitz条件.g是方程右端扰动所产生的项,g<δ<<1,(t,x)∈G.设其解分别为x(t)和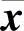 (t),t∈[a,b].∀ε>0,我们来求δ(ε)>0使得只要g<δ,便有
(t),t∈[a,b].∀ε>0,我们来求δ(ε)>0使得只要g<δ,便有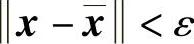 成立.事实上,利用两个Cauchy问题所对应的积分方程可得(t>t0)
成立.事实上,利用两个Cauchy问题所对应的积分方程可得(t>t0)
由Gronwall引理得
则对∀ε>0, ,当g<δ时,有
,当g<δ时,有
定理1.1.9 (解对参数的连续依赖性)考察Cauchy问题
若f关于t,x,μ在区域G⊆R×Rn×Rm内连续,对x满足局部Lipschitz条件,并设对于给定的μ0∈Rm,式(1.1.14)的解在闭区间[a,b]上存在,则对使μ-μ0<<1的μ,问题(1.1.14)的解仍在[a,b]上存在,而且对μ连续.
证 此定理的结论可以直接由定理1.1.8得出.为此,将式(1.1.14)中的方程改写为
记 g(t,x,μ)=f(t,x,μ)-f(t,x,μ0).
由于f关于μ连续,故当μ-μ0<<1时,有g<<1,再应用定理1.1.8便得解对μ连续的结论.
定理1.1.10 (解对初值和参数的可微性)设f(t,x,μ)对t是r-1次连续可微的,对x和μ是r次连续可微的,则Cauchy问题(1.1.14)的解x=x(t,t0,x0,μ)对t,t0,x0,μ而言是r次连续可微的.
定理1.1.11 (解对初值和参数的解析性)设f(t,x,μ)在区域
G={(t,x,μ)t-t0<a,x-x0<b,μ-μ0<c}是t,x,μ的解析函数,则Cauchy问题(1.1.14)的解x=x(t,t0,x0,μ)也是t,t0,x0,μ的解析函数.
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。