为了用有限差分法求解常微分方程,即式(5-84),可首先将管道在长度方向离散成N等份,每一等份的长度为Δx,每隔Δt时间计算一次水击压力的分布,则在长度方向和时间方向的离散可以形成一个计算网格,见图5-12。如果计算的时间步长取为Δt=Δx/a,则网格的对角线斜率为+1/a或-1/a,即满足式(5-81)或式(5-82)中的第二个方程。如果A点的变量v和H是已知的,那么沿着C+方向的特征线从A到P进行积分(同时应注意adt/g=dx/g的问题且应用流量Q代替流速v)可得式(5-83),即

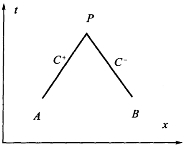
图5-11　特征线

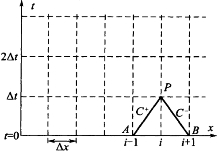
图5-12　单一管道求解的x-t网络

同样,对方程组

可得式(5-84),即

式(5-83)和式(5-84)中所包含的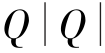是与x有关的变量,在近似计算中可用A点或B点的值表示。若Δx取得足够小则其一次近似即可满足要求,即代入A、B值后可得式(5-85)和式(5-86),即

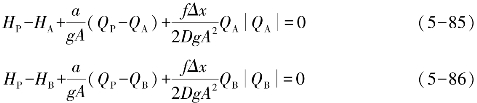
上面两个方程,即式(5-85)和式(5-86)中,A点和B点的变量值是已知的,而未知量只有HP和QP,故通过两个方程联立即可以求解出结果。发生水击过程之前或发生之初(即t=0时)管道中的水流呈稳定流状态(各点的H、V是已知的),在t=Δt时刻管道中任一点的流动状态可由式(5-85)和式(5-86)解出,进而可以再对t=2Δt时刻的流动状态进行计算。需要注意的是,管道两端的边界点由于只能利用式(5-85)和式(5-86)中的一个方程,因此还必须应用管道的边界条件才能求解,此时可引入流量与流速的关系Q=VA(A为管道断面积)并将计算过程中与管道特性有关的常数进行简化,即令,则式(5-85)和式(5-86)可以分别写成式(5-87)和式(5-88),即

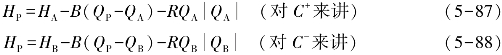(www.daowen.com)

对于特征网格上任意截面i点,上述两方程,式(5-84)和式(5-85),可改写为

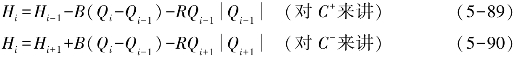
令式(5-91)和式(5-92)成立,即

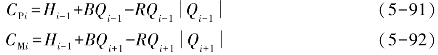
将式(5-91)和式(5-92)代入式(5-84)和式(5-85)可得

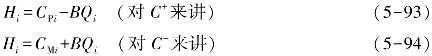
因此,根据式(5-93)和式(5-94)可以获得最终计算结果,即

或

通过观察图5-12中的网格不难看出,系统中的两个端点是从第一时步以后开始影响内部点的。因此,为了求得任意时刻的解必须引入相应的边界条件。