(1)水击的基本方程　对有压管道来讲,不论在何种情况下都应满足水流的运动方程及连续方程,当水管材料、厚度及直径沿管长不变时,其运动方程为

将管道材料及水体当作弹性体考虑时其连续方程为

式中,H为压力水头;v为管道中的流速(向下游为正);a为水击波传播速度;f为水流摩擦阻力系数;D为管道直径;x为距离(其正方向与流速取为一致);t为时间。各个符号的单位同前。

式(5-2)、式(5-3)中,因流速v与波速a相和项。另外,为简化计算可使方程线性化并忽略摩擦阻力影响。当x轴改为取阀门端为原点、向上游为正时(见图5-2),式(5-2)、式(5-3)可简化为

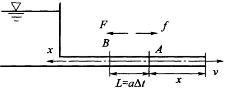
图5-2　水击计算示意图

式(5-4)和式(5-5)为一组双曲线形偏微分方程,其通解为

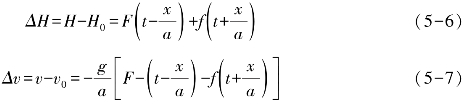
式中,H0、v0分别为初始水头和流速;F、f分别为两个波函数(其量纲与水头H相同,故可视为压力波);F(t-x/a)表示以波速a沿x轴负方向传播的压力波(即逆水流方向移动的压力波,称为逆流波);f(t+x/a)表示以波速a沿x轴正方向传播的压力波(即顺水流方向移动的压力波,称为顺流波);各个符号的单位同前。

这样,可认为任何断面任何时刻的水击压力值等于两个方向相反的压力波之和,而流速值则为两个压力波之差再乘以-g/a。如果知道了t时刻在x位置处的水击波函数F(t-x/a),则当时间变为t1=t+Δt时,x1=x+aΔt处的逆流波函数为

若式(5-8)的值不变,则证明F(t-x/a)沿逆水流方向的传播特性。反之,若研究发现t1=t+Δt时刻在位置x1=x-aΔt处为顺流波函数,则可以证明f(t+x/a)沿顺水流方向的传播特性。(www.daowen.com)

(2)水击计算的连锁方程　若已知断面A(见图5-2)在时刻t的压力为HAt、流速为vAt,由式(5-6)和式(5-7)消去f后,可得

同理,可写出Δt=L/a时刻后B点的压力和流速的关系,即比数量较小,故可忽略

由于

故由式(5-9)、式(5-10)可得

同理,有

式(5-12)和式(5-13)称为水击连锁方程。连锁方程给出了水击波在一段时间内通过两个断面的压力和流速的关系。但其前提是应满足水管的材料、管壁厚度、直径沿管长不变。水击连锁方程[式(5-12)和式(5-13)]可用相对值表示为

式中,为管道特性系数;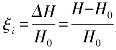为水击压力相对值;为管道相对流速。