前已叙及,明敷钢管通常是敷设在一系列支墩上的,为改善钢管的受力条件及保持管壁的外压稳定,有时需要在管壁上加设支承环和加劲环。钢管承受的荷载分为径向力、轴向力、法向力,可以利用叠加原理对其进行应力分析。在管重和水重作用下钢管相当于一根连续梁,在轴向力作用下钢管可当作轴向受压构件计算,而径向力作用只会引起钢管的环向变形。根据受力特点,管身的应力分析可选择四个基本断面,见图4-15。图4-15中,(1)—(1)断面在跨中,只有弯矩作用且弯矩最大、剪力为零、无局部应力,受力最简单;(2)—(2)断面位于支承环旁管壁膜应力区的边缘,弯矩和剪力共同作用,无局部应力,受力比较简单;(3)—(3)断面是加劲环及其旁管壁,由于加劲环的约束,存在局部应力;(4)—(4)断面是指支承环及其旁管壁,应力最复杂,弯矩和剪力(支承反力)共同作用,存在局部应力,在压力钢管的应力分析中其坐标系规定为轴向x、径向r、环向θ(见图4-16)。

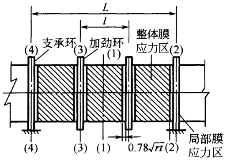
图4-15　明敷钢管应力分析的几个断面

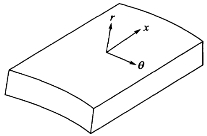
图4-16　管壁应力计算坐标系

(一)跨中段面(1)—(1)的管壁应力

跨中段面属于膜应力区,其特点是弯矩最大、剪力为零,故主要计算其径向应力、切向(环向)应力和轴向应力。

(1)径向应力σr的计算方法　水管的内表面承受内水压力,所以内表面的径向应力等于该处的水压强,即σr=-γH“-”表示压应力。管壁外表面的σr=0。由于径向应力的数值比较小,所以应力计算中可以忽略。

(2)切向(环向)应力σθ1的计算方法　设压力水管中心处的水头为H,而水管轴线与水平面的夹角为α,则在管壁中任意一点(该点半径与管顶半径的夹角为θ,见图4-17)的水头为H-rcosαcosθ。在管壁中取出一段微圆弧,其圆周长为沿轴线方向取单位长度,则由力的平衡(见图4-18)条件可以推导出管壁中的切向拉力T和切向应力σθ1,即

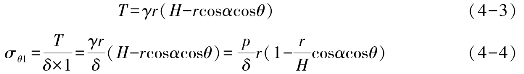
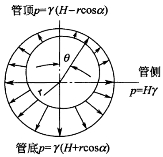
图4-17　管壁上内水压力的分布

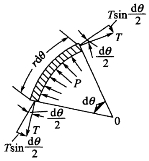
图4-18　管壁微圆弧的受力平衡

式中,p内水压强;δ为管壁计算厚度;H为计算水头;α为管轴线倾角;θ为管壁中任意一点半径与管顶半径的夹角;r为水管半径。各个符号的单位同前。

(3)轴向应力σx。的计算方法　跨中段面的轴向应力由两部分组成,即法向力作用引起的管壁轴向应力σx1和轴向作用力引起的轴向应力σx2。

①法向力作用引起的管壁轴向应力σx1。可将水重和管重的法向分力视为均布荷载,则钢管的受力与多跨连续梁类似,其变形以弯曲为主,并在管壁上产生弯曲正应力与剪应力。相邻两镇墩之间的压力钢管放置于支墩之上,支墩相当于连续梁的中间辊轴支座,最下端的镇墩相当于固定端,上端伸缩节处可近似认为是自由端。在均布荷载作用下,三跨连续梁的弯矩和剪力见图4-19(其他情况则可用结构力学方法求出或查规范计算),这样管壁横断面上任意一点的轴向应力为

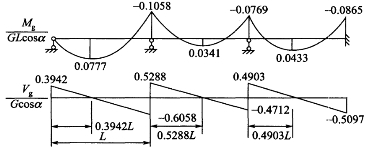
图4-19　三跨连续梁截面内力

式中,M为水重和管重的法向分力作用下连续梁的弯矩(钢管底部受拉为正);W为连续梁(空心圆环)的断面模数(W=πr2δ)。

②轴向力引起的轴向应力σθ2。在轴向力合力∑A作用下管壁中产生的轴向应力为σθ2,若管壁的断面积为F,则F=πDδ,故有

式中,“—”表示压应力;一般情况下;∑A为压力(即σθ2为压应力);D为管道直径。

(4)剪应力τxθ的计算方法　由于跨中断面的剪力为零,所以该断面τxθ=0。

(二)支承环旁管壁膜应力区边缘(2)—(2)断面的管壁应力

(2)—(2)断面虽然靠近支承环,但却在支承环的影响范围之外(即不考虑支承环对管壁的约束作用),为了安全起见可认为该断面的弯矩和剪力与支承环断面相等。对于连续梁,跨中断面和支承环断面的管道弯矩方向相反,故可用式(4-5)计算弯曲应力。此外,支承环处还存在剪力V,在垂直于管道轴线的横断面上剪应力的计算公式为

式中,V为管重和水重的法向分力作用下连续梁的剪力;SR为计算点以上管壁环形截面积对重心轴的静矩(SR=2δr2sinθ);b为受剪截面宽度(b=2δ);J为截面惯性矩(J=πD3δ/8=πr3δ)。各个符号的单位同前。

当θ=0°(管道顶部)和θ=180°(管道底部)时,τxθ=0;当0=90°(管道侧面中点)时,τxθ=2V/F(达到最大值)。τxθ的分布见图4-18(图4-18为以上各应力的综合图)。断面(2)—(2)的其他正应力σr、σθ和σx均与断面(1)—(1)相等但符号不尽相同。

(三)加劲环及其旁管壁断面(3)—(3)的管壁应力

⑴轴向应力σθ3的计算方法　由于加劲环的存在,管壁在内水压力作用下的径向变形受到了限制,因而将产生局部应力,其变形状态见图4-20(a),加劲环对管壁约束的影响范围每侧为l′(l′又称等效翼缘宽度),根据弹性理论分析可得

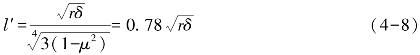
式中,μ为钢材的泊松比。其余各符号的含义及单位同前。

对于l′范围以外的管壁可认为其不受加劲环的影响(即不存在局部应力)。在计算时,加劲环有效断面面积F等于其自身净断面F′加上两侧各长为0.78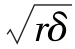的管壁面积。在内水压力作用下其变形具有轴对称特性,因此管壁圆周上各处的弯矩和剪力值都相等。设想将加劲环与管壁切开,根据变形相容条件可以证明,在切口处存在着均布的径向弯矩M和剪力V,见图4-20(b)。设在内水压力p和管壁传来的剪力V作用下,加劲环向外径向变位为Δ1;加劲环影响范围以外的管壁向外径向变位为Δ2;如果没有M和V的作用则全部管壁都将有相同的变位Δ2;但在M和V作用下,钢管与加劲环连接处的变位应该与加劲环的变位相同(等于Δ1)。可以看成是在M和V作用下使钢管在断面(3)—(3)处发生一个变位等于Δ3。根据变形连续条件有Δ3=Δ2-Δ1,同时管壁在M和V作用下没有角变位(转角)。

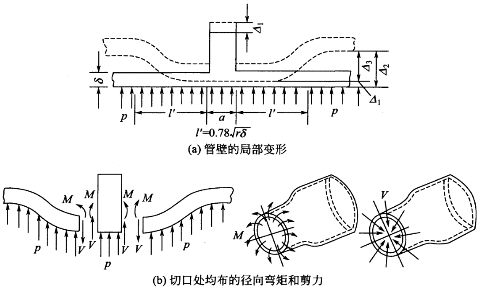
图4-20　加劲环及其旁管壁变形示意

式中,E为钢材弹性模量。其余各符号的含义及单位同前。

②Δ1的计算。用前述类似的方法可以推导出Δ1,即

式中,a为加劲环宽度;F′为加劲环净截面积(不包括管壁翼缘)。其余各符号的含义及单位同前。

③Δ3的计算。根据弹性理论,M与V之间存在的关系可表达为

在M与V共同作用下,该处管壁的径向变位减小Δ3为

式中,k为等效翼缘宽度的倒数,即

根据连续条件Δ3=Δ2-Δ1,将式(4-10)～式(4-12)代入可得

再将代入式(4-13),化简后可得

(www.daowen.com)

将式(4-14)代入式(4-11)得

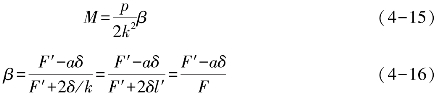
式中,F为加劲环有效截面积(包括管壁的等效翼缘)。其余各符号的含义及单位同前。

最后,可得局部弯矩M产生的管壁局部轴向应力σx3为

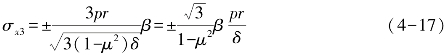
若取μ=0.3,则有

式(4-18)中的正号代表管壁内缘受拉,负号代表管壁外缘受压。由于0≤β≤1,故当F′很大时β≈1,而没有加劲环时F′=aδ、β≈0。

(2)剪应力τxr的计算方法　前已叙及,分布剪力V在加劲环旁管壁内产生剪应力为τxr,τxr的作用方向指向管中心,其值可用公式τxr=1.5βp/kδ(管壁中面)或τxr=0(管壁内、外缘)计算。一般情况下,τxr值较小且管壁总应力的控制点在管壁内外缘,故τxr可忽略不计。

(3)切向应力σθ2的计算方法　加劲环净截面除承受径向的均匀内水压力pa外,还承受外侧径向剪力2V,见图4-19(a),则总切向拉应力为

将式(4-14)代入式(4-19)得

根据式(4-16)可得

将式(4-21)代入式(4-20)可得

(4)剪应力τθx的计算方法　由管重和水重法向分力在管壁中引起的剪应力τxθ可用式(4-7)计算,而由剪应力互等定理可知

断面(3)—(3)的轴向应力σx1、σx2和剪应力τxθ的计算均与断面(2)—(2)相同。综合断面(3)—(3)各应力方向和分布见图4-21。

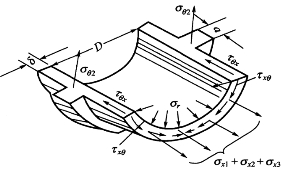
图4-21　加劲环断面管壁应力分布和方向示意

(四)支承环及其旁管壁断面(4)—(4)的管壁应力

支承环与加劲环从形式上看都是一个套焊在管壁外缘的钢环,因此断面(4)-(4)的管壁应力计算均与断面(3)-(3)相同。但支承环由于承担管重和水重法向力Q而会在支墩处引起支承反力R,从而在支承环内产生附加应力。随着支承方式和结构的不同,其应力状态也不同。

(1)支承环的支承方式　大、中型水电站明敷钢管上的支承环支承方式有侧支承和下支承两种形式,见图4-22。图4-22中点画线为支承环有效截面重心轴(它与圆心距离为半径R),支墩支承点至支承环截面有效重心轴距离为b,支承反力为Q/2cosα。

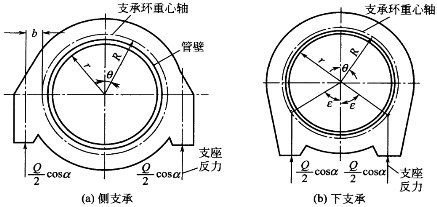
图4-22　支承环支承方式

(2)支承环内力计算　支承环的内力计算目前常采用结构力学中的弹性中心方法进行。因为钢管断面是一个对称圆环,是一个三次超静定结构,故可用弹性中心法计算支承环上各点的内力。当采用侧支承时,可令支承反力离支承环重心轴距离为b(根据分析,在设计时取b=0.04R可使环上最大正弯矩与最大负弯矩接近相等,则钢材性能得到最充分的发挥),采用下支承时一般取ε=30°～90°较经济,符号ε的意义见图4-21(b)。

①侧支承式支承环的内力计算。支承环所承受的荷载主要是管重和水重法向分力产生的剪力(表现为支承环两侧管壁上的剪应力τxθ)以及支墩两侧的反力0.5Q(当然还有支承环自重,但相对较小可以不计)。钢管一般都是倾斜布置的,故支承反力为0.5Qcosα。管重和水重在支承环两侧管壁上产生的剪应力均为τxθ因此沿管壁圆周单位长度上作用在支承环上的剪力为

进行支承环截面的内力计算实际上是要计算一个封闭圆环各断面上的弯矩MR、剪力TR和轴力NR(其计算简图如图4-23所示),利用结构力学中的弹性中心法可将圆环顶部切开加上内力TG和MG(由于圆环是对称图形,该处没有剪力)并把内力移到弹性中心,令弹性中心处的力矩为M0、推力为T0,则由弹性中心法原理可得

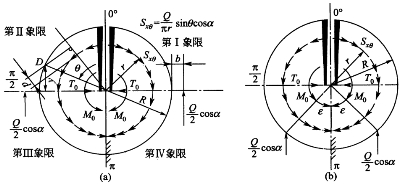
图4-23　支承环计算简图

式中,MS为圆弧上各点的静定力矩(以顺时针方向为正);y为圆弧的纵坐标;ds为弧长的微分。其余各符号的含义及单位同前。

求出弹性中心处的M0、T0后,即可得到环顶切口处的内力MG、TG,进而可推求出封闭圆环(支承环)任一断面上的内力。导出的内力MR、TR和NR在一些特殊点处的计算公式见表4-5,从表4-5中可以看出,支承环内力除取决于它的几何尺寸及荷载Q、Sxθ以外,还与支点的位置b有关(当b=0.04R时支承环各断面的内力分布情况如图4-24所示,图中弯矩画在受拉一边,正的M0表示支承环外侧受拉,正的NR表示拉力,正的TR方向见图中箭头)。

表4-5　支承环内力计算公式

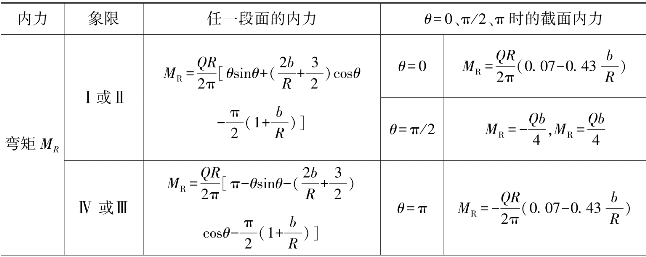
续表

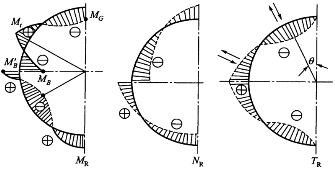
图4-24　b=0.04R时支承环内力图

②下支承式支承环的内力计算。下支承环支点位置可通过ε角度确定,见图4-23(a),仍可用弹性中心法计算内力,计算简图见图4-23(b)。支承环任意断面内力计算公式可查《水电站压力钢管设计规范》(DL/T 5141)。不论是侧支承或是下支承若需要考虑地震影响时,还需计算横向地震力作用下产生的内力,计算公式可参考《水电站压力钢管设计规范》(DL/T 5141)。

计算出支承反力产生的弯矩MR、轴力NR和剪力TR后,它们所产生的应力分别为(见图4-23)

式中,NR为支承环横截面上的轴力;MR为支承环横截面上的弯矩;ZR为计算点与重心轴的距离;JR为支承环有效截面对重心轴的惯性矩;WR为支承环有效截面对重心轴的面积矩;TR为支承环横断面上的剪力;SR为支承环有效截面上计算点以外部分对重心轴的静矩;a为支承环腹板厚度;F为支承环有效截面积(包括管壁等效翼缘)。断面(4)—(4)各应力的方向和分布见图4-24,四个断面的应力计算公式见表4-6。

表4-6　明敷钢管应力计算公式