1.数据加密概述

即使安装了防火墙、入侵检测系统及杀毒软件，也难以完全防止信息被窃取。为此，可以再实施一种安全措施——加密(Encryption)。

加密是把明文通过混拆、替换和重组等方式变换成对应的密文。明文是加密前的信息，有着明确的含义并为一般人所理解。密文是对明文加密后的信息，往往是一种乱码形式，一般人很难直接读懂其真实含义，密文需要按加密的逆过程解密成明文后，才能理解其含义。所以，在信息传输前，甲乙双方约定好加密、解密方式，甲方对明文加密后以密文形式传输给乙方，乙方收到密文后按约定方式解密还原成明文，就能理解甲方所发信息的真实含义。在信息传输过程中，即使有甲乙之外的第三方通过非法途径窃取了传输的密文信息，如果不能同时获取加密、解密约定，是很难直接从密文读懂其真实含义的。所以，加密技术进一步保证了信息传输的安全性。

当然，如果加密、解密约定也被第三方窃取，那信息传输的安全也就丧失了，这时可以说第三方破译了甲乙双方的密文传输，这种保密与窃密的斗争在情报战题材的电视剧和电影中经常出现，甲乙双方极力想办法保密自己的信息传输，有时经常更换加密、解密方式，而第三方(敌方)也在尽力想办法破译甲乙双方的信息传输。

图灵就是破译密码的高手，在第二次世界大战期间，图灵在英国外交部的一个下属机构工作，使用自己研制的译码机破译了德军不少的机密情报，为盟军战胜德国法西斯立了大功，战后被授予帝国勋章。

加密的历史一直可以追溯到文字通信的开始，一些很古老的加密方法在当时起了重要作用，当然现在已不再使用这些加密方法，特别是在计算机的辅助下，这些加密方法很容易破译，但介绍这些方法对于理解加密的基本原理是很有帮助的。

2.古典加密方法

(1)恺撒密码

顾名思义，恺撒密码(Caesar Cipher)是由古罗马人恺撒发明的，通过移位的方式实现对原始信息的加密。恺撒密码也称为单字符替换，即对不同位置的字符采用相同的移位方式。

【例4.1】采用恺撒密码对computer进行加密。

设置26个英文字母与数字的对应关系如下：

a b c d e f … u v w x y z

0 1 2 3 4 5 … 20 21 22 23 24 25

对明文中的每个字符右移一位(变换成下一个字符)就可以实现对明文的加密。

对于英文单词computer中的每个字符右移一位，就变换成了字符串dpnqvufs，computer的含义是“计算机”，dpnqvufs的含义就难以理解了。

从这个例子可以看出，加密是一种变换技术，把人们能理解的明文变换成不能理解的密文。

这种简单移位的加密方法是很容易破译的。用最简单的思路就可以对密文进行右移1位、2位、3位……，左移1位、2位、3位……的逐一试探，就能破译。特别是现在借助于计算机，就更容易破译了。

(2)多字符替换

单字符替换的优点是实现简单，缺点是容易破译。稍微复杂一点的方式是多字符替换，即不同位置的字符采用不同的替换方式。

【例4.2】采用(+1，-1，+2)的替换方式对computer加密。

对明文中的第1个字符右移1位，第2个字符左移1位，第3个字符右移2位，第4个字符又是右移1位，如此进行下去，完成明文中所有字符的替换。

对computer进行(+1，-1，+2)模式的多字符替换后的密文为dnoqtvfq，密文的含义仍是难以理解的。

破译这种加密方式难度要大一些，特别是手工破译，工作量比较大。但借助于计算机，还是比较容易破译的。

(3)二进制运算

对于二进制数，除了可以进行算术运算外，还可以进行逻辑运算，主要有与(AND)、或(OR)、非(NOT)和异或(XOR)等。

AND的运算规则：对应位都是1，结果位为1，否则结果位为0。

OR的运算规则：对应位都是0，结果位为0，否则结果位为1。

NOT的运算规则：1变成0，0变成1。

XOR的运算规则：对应位相同，结果位为0，对应位不同，结果位为1。

【例4.3】二进制运算示例。

10101100 AND 01101011=00101000

10101100 OR 01101011=11101111

NOT 10101100=01010011

10101100 XOR 01101011=11000111

其中，异或运算有一个对加密来说很有用的特性：一个数和另外一个数进行两次异或运算，结果又变回这个数本身，即A XOR B XOR B=A。

例如，10101100 XOR 01101011 XOR 01101011=10101100。

【例4.4】采用异或运算对computer 进行加密。

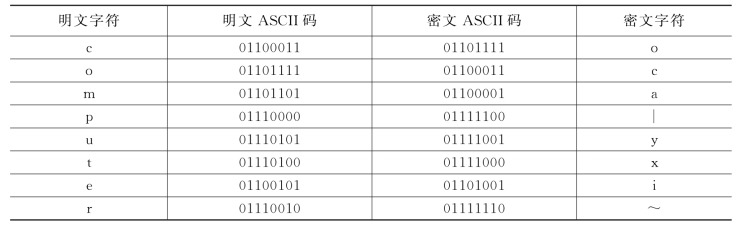
对于computer，首先以ASCII码的形式把每个英文字符转换成二进制数。选定一个8位的二进制数00001100作为加密密码(也称为加密密钥)，每个明文字符的ASCII码都分别和这个密钥进行异或运算(加密)，变换成密文，接收方也用这个相同的密钥再进行一次异或运算(解密)，还原成明文。

加密结果如表4-2所示。加密前的明文为computer，加密后的密文为oca︱yxi～。读者可自行对密文进行解密。(www.daowen.com)

表4-2 基于异或运算的computer加密结果

3.现代加密方法

(1)私钥加密

私钥加密指加密和解密使用同一个密钥，而且这个密钥属于通信的甲乙双方私有，不能公开让第三方知道。如例4.4中的00001100，既是加密密钥，也是解密密钥。私钥加密也称为单密钥加密或对称密钥加密，形象地说锁信箱和开信箱用的是同一把钥匙，密钥要保密存放，一旦密钥被攻击者窃取，就无密可保。

代表性的私钥加密算法是DES算法。数据加密标准(Data Encryption Standard，DES)是由IBM公司在20世纪70年代开发的，曾经得到了广泛的应用。

DES算法的加密过程如下：

1)待加密数据被分为64位(二进制位)大小的数据块。

2)对第一个64位的数据块进行初始变换，即对64位的数据按位重新组合，如将第58位换到第1位，第50位换到第2位，……

3)将换位后的数据与密钥进行计算(如异或运算)，这样的计算共进行16轮，每一轮使用一个不同的密钥，这16轮的密钥合称DES算法的加密密钥，也是日后解密的密钥，如果不是密钥持有人有意或无意的泄露，靠技术手段破译是有一定难度的。

4)把经过16轮加密的数据再进行换位操作，这时的换位是初始换位的逆操作，如第1位经初始换位后换到了第40位，经逆初始换位，再把第40位换回到第1位。

5)逆初始换位后的结果是第一块数据加密后的密文。

6)对其他每块数据都进行与第一块数据类似的处理，得到全部明文对应的密文。

1998年之后，不再使用DES，改用更难以破译的AES(Advanced Encryption Standard)算法。

(2)公钥加密

公钥加密是与私钥加密相对的一种加密方法。公钥加密有两个不同的密钥，一个用于加密，是公开的，称为公钥；另一个用于解密，是不公开的，称为私钥。可以作这样的设想：我有一个保密信箱，锁信箱和开信箱用的是两把不同的钥匙，锁信箱的钥匙是公开的，就挂在信箱上，谁要是想把信件秘密给我，就可以放在信箱中，并用公开的钥匙锁上信箱。公开的钥匙只能锁信箱，不能打开信箱，打开信箱用的是另一把保密的钥匙，我自己拿着，其他人不知道。这样任何人都可以往我的保密信箱中投放秘密信件，但只有我自己能打开信箱取出信件，从而实现了秘密通信。

代表性的公钥加密算法是RSA算法，是由R.L.Rivest、A.Shamir和L.M.Adleman于1978年在美国麻省理工学院研发出来的，为此，三人共同荣获2002年度的图灵奖。

RSA算法中，选定密钥的过程如下：

1)选择两个互异的大素数p和q；

2)使n=p×q，t=(p-1)×(q-1)；

3)取一个整数e，使其满足1＜e＜t，且gcd(t，e)=1；

4)计算d，使其满足(d×e)mod t=1；

5)以{e，n}为公钥，{d，n}为私钥。

其中，gcd是求最大公约数函数，mod是求余数函数。

RSA算法的加密过程如下：

将二进制位串形式的明文信息分组，使得每个分组对应的十进制数小于n，即分组长度小于log2n，然后对每个明文分组m作加密计算，得到其对应的密文c=m e mod n。

RSA算法的解密过程如下：

对每个密文分组进行解密计算，还原成其对应的明文m=c d mod n。

【例4.5】采用RSA算法对computer进行加密。

选p=7，q=17。则n=7×17=119，t=6*16=96。

取e=5，满足1＜e＜t，且gcd(t，e)=1；满足(d×e)mod t=1条件的d=77。

所以，{5，119)为公钥，(77，119}为私钥。

把computer转换成十进制形式表示的ASCII码，然后每个字符的ASCII码与私钥{77，119}进行加密计算，就能得到computer的密文，如表4-3所示。

表4-3 基于RSA算法的computer加密结果

如995 mod 119=29，其他字符的加密解密类似。

RSA的安全性分析：在RSA算法中，{e，n}为公钥，{d，n}为私钥。在n大到一定程度时，由{e，n}得到d的计算量是很大的，因为把n分解成两个互异的素数p和q是困难的(通过把n分解为p和q，才能由e计算出d)。RSA算法实际上是利用了数论领域这样一个事实：虽然把两个大素数相乘得到一个合数是非常容易的，但要把一个很大的合数分解为两个素数却十分困难，至今没有任何高效的分解方法。

当然，随着新的分解方法和高性能计算机的不断出现，人们的计算能力也在不断提高，RSA-129(n为129位的十进制数或428位的二进制数)经过8个月的计算于1994年4月被成功分解，RSA-155(n为155位的十进制数或512位的二进制数)于1999年8月被成功分解，得到两个78位的十进制表示的素数。就目前的分解方法和计算能力来看，选择1 024～2 048位之间的二进制数作为n在一段时间内是安全的。