对于初学者来说，算法(Algorithm)可能是第一次听到，但其实我们很早就已经接触过算法了，算法一直在我们身边。相信大家都听说过农夫过河的问题，一个农夫带着一只狼、一只羊和一棵白菜过河，河边只有一条船，由于船小，农夫一次只能带其中的一样过河，如图3-26所示。如无人看管，狼要吃羊，羊要吃菜。问农夫如何安排过河，才能使得羊、菜都安然无恙?

图3-26 农夫过河实例图

(1)农夫带着羊渡过河去；

(2)农夫划船回来；

(3)农夫带着菜渡过河去；

(4)农夫带着羊划船回来；

(5)农夫带着狼渡过河去；

(6)农夫划船来；

(7)农夫带着羊渡过河。

农夫过河其实就是经典的算法问题，这个算法解决了农夫过河的问题，所以说，算法听起来高大上，实际上在我们生活中随处可见，每一天我们都会用到各种算法来解决我们遇到的实际问题，只是你还不具备算法的思维。

算法是解决特定问题求解的步骤的描述，在计算机中表现为指令的有限序列，其中每一条指令表示一个或多个操作。

1.算法的五个重要特性

算法反映解决问题的步骤，不同的问题需要用不同的算法来解决，同一问题也可能有不同的解决办法，但是一个算法必须具有以下特性：

(1)有穷性：一个算法必须总是在执行有穷步之后结束，并且每一步都可在有穷时间内完成。

(2)确定性：算法中每一条指令必须有明确的含义，读者理解时不会产生二义性。并且，在任何情况下，算法只是唯一的一条执行路径，即对于相同的输入只能得出相同的输出。

(3)可行性：一个算法是可行的，即算法中描述操作都是可以通过已经实现的基本运算执行有限次来实现的。

(4)输入项：一个算法有零个或多个的输入，这些输入取决于某个特定的对象的集合。

(5)输出项：一个算法有一个或多个的输出，这些输出和输入有着某些特定关系的量。

综上来看，拍黄瓜就是一个算法，它就是一个饭菜制作的流程，解决我们如何做饭的问题。拍黄瓜的算法步骤为：

(1)黄瓜洗干净。

(2)放在案板上，用刀拍开，切小块。

(3)蒜切末，花生用刀碾碎。

(4)黄瓜加入蒜末、花生粒、生抽、芝麻油、香醋，充分搅拌均匀入味，即可。

按照算法的定义，拍黄瓜具有算法的五个特征：

有穷性：拍黄瓜有明确的四个步骤。

确定性：每个步骤目标明确。

输入项：黄瓜、蒜、花生、生抽、芝麻油、香醋。

输出项：拍黄瓜这道菜。

可行性：每个步骤目标明确，能够在有限时间内完成。

2.算法设计的要求

比如你要从上海到北京，中间可能有多种换乘方案，是选速度最快的，还是选最省钱的，还是平衡的，制订换乘方案就是算法。

所以，对于一个问题来说，解决问题的算法并不是唯一的，不同算法有好有坏，掌握好的算法会对编程有极大的好处，通常设计一个好的算法应考虑达到以下目标：

(1)正确性：算法的正确性是指算法至少应该具有输入、输出和加工处理无歧义性、能正确反映问题的需求、能够得到问题的正确答案。

但是算法的“正确” 通常在用法上有很大的差别，大体分为以下四个层次：(www.daowen.com)

1)算法程序没有语法错误。

2)算法程序对于合法的输入数据能够产生满足要求的输出结果。

3)算法程序对于非法的输入数据能够得出满足规格说明的结果。

4)算法程序对于精心选择的，甚至刁难的测试数据都有满足要求的输出结果。

对于这四层含义，层次1)要求最低，但是仅仅没有语法错误实在谈不上是好算法。而层次4)是最困难的，我们几乎不可能逐一验证所有的输入都得到正确的结果。

因此算法的正确性在大部分情况下都不可能用程序来证明，而是用数学方法证明的。证明一个复杂算法在所有层次上都是正确的，代价非常昂贵。所以一般情况下，我们把层次3)作为一个算法是否正确的标准就可以了。

(2)可读性：算法设计是为了便于阅读、理解和交流。可读性高有助于人们理解算法，晦涩难懂的算法往往隐含错误，不易被发现，并且难以调试和修改。我们写代码的目的，一方面是让计算机执行，但还有一个重要的目的是便于他人阅读，让人理解和交流，自己将来也可能阅读，如果可读性不好，时间长了自己都不知道写了些什么。可读性是评价算法好坏很重要的标志。

(3)健壮性：一个好的算法还应该能对输入数据不合法的情况作合适的处理。比如输入的时间或者距离不应该是负数等。当输入数据不合法时，算法也能作出相关处理，而不是产生异常或莫名其妙的结果。

(4)时间效率高和存储量低：时间效率指的是算法的执行时间，对于同一个问题，如果有多个算法能够解决，执行时间短的算法效率高，执行时间长的算法效率低。存储量是指算法在执行过程中需要的最大存储空间，主要指算法程序运行时所占用的内存或外部硬盘存储空间。设计算法应该尽量满足时间效率高和存储量低的需求。在生活中，人们都希望花最少的钱，用最短的时间，完成同样的事，算法也是一样的思想，最好用最少的存储空间，花最少的时间，办成同样的事就是好的算法。

3.算法的应用

算法已经显露了它的锋芒，并且进入我们的生活中，甚至已经开始改变着世界。一个程序的核心在于算法，比如说运行一个软件的速度在计算机硬件性能相同情况下，软件的算法起到了几近决定性作用。无论是现实生活中解决实际问题，还是解决编程中遇到的问题，有无算法驱动将会产生极大的差别。我们将介绍一些常用算法的应用，来显示有无算法的区别，以此来证明算法的价值。

(1)二分查找

小明是一个赌球爱好者，最近他连续几次提前收到了预测赌球结果的邮件，奇怪的是每一次都预测得非常准确，从一开始由于不屑而错失良机，到渐渐深信不疑，直到最后给邮件发送方汇了巨款才发现上当。那么骗子是如何从几万或几十万用户中寻找这些“幸运儿”的呢?

这里骗子使用了二分法的查找思想，首先骗子将所有用户分为两批，其中一批发送甲队赢的邮件，另外一批发送乙队赢的邮件。然后再从猜对的那一批赌球爱好者中继续分为两批，采用同样的方式，如此反复，如果拥有足够多的赌球爱好者信息，那么总是会有人接收到完全预测正确的邮件。

最正统的二分法是每次都可以排除掉一半的情况，这样的寻找效率是很高的。比如要在1～100的数字中询问出某一个特定的数字，我可以先问，这个数字是否大于50?这样无论是或者不是，我都可以排除掉一半的数字(50之前的被排除，或者50之后的被排除)。假如回答不是，接着我可以问是否大于25?又可以排除掉一半。这样下去，很快就会找到那个数字。

如图3-27所示，我们要寻找88，先看最中间的51，小于51，那么我们就可以将51及其左边的全部排除掉，然后剩下的中间数字是89，大于88，然后将89及其右边的去掉，如此反复，我们最终可以找到88。

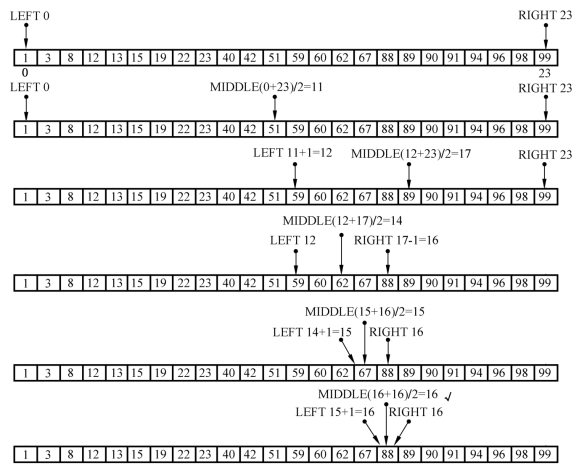
图3-27 二分查找

对于一个长度为N的数组，简单顺序查找(从头开始查找)最多需要N步；二分查找最多只需要log2 N步，二分查找相较于简单顺序查找，极大地提高了效率。

(2)贪心算法

现在流行网上购物，假如你想要开一家网站，在全国各省都有生意，现在面临发快递的问题，假设现在的基础物流不是很完善，每家快递公司只能覆盖很少几个省，那么你该如何在覆盖全国所有个省级行政区的情况下，选择最少的快运公司?

这个问题看起来不是很难，但是如果我们不使用算法来直接挑选快递，假如有50家快递就会面对上亿次选择，这简直就是不可能解决的问题。

对于一些比较复杂的问题，这时候往往会使用贪心算法：每步操作都选择局部最优解，最终得到的往往就是全局最优解。这似乎是想当然的做法，但是在很多情况下真的行之有效。我们可以使用贪心算法来解决这个问题：选择一家覆盖了最多未覆盖省的快递公司。反复重复直到所有省市被覆盖，这样很快就会选择出快递公司。

假如快递公司目前覆盖的中国省级行政区如表3-3所示，我们可以使用贪心算法来选择快递，首先邮政可以覆盖的省份最多，所以我们首先选择邮政，然后在剩下的省份中，我们选择使用中通快递，之后在剩余的省份中覆盖最多的是天天快递，依此类推，我们可以找到最终的快递搭配，可能这种搭配并不是最合理的，但是通过这样的方式我们可以快速找到能够覆盖中国所有省级行政区的组合，然后我们会发现这样的搭配组合也不错。

表3-3 快递公司覆盖地区

(3)插入算法

我们在闲暇的时间经常玩扑克牌，每当抓完牌之后，都要将牌从小到大或者从大到小进行整理，此时我们在不经意间使用了插入排序算法，如图3-28所示。

图3-28 插入算法实例图

假如将扑克牌以从小到大的方式进行排列，此时插入排序的思想是这样的：将第二张牌插入第一张牌中，如果第二张牌大于第一张牌就放到右边，小于第一张牌就放到左边。然后将第三张牌按照同样的方式插入已经排好序的两张牌中，依此类推，最后就会将所有的牌排好序。

如图3-29所示，现在有一个无序的线性表，第一趟插入：将第2个元素插入前面的有序子序列，此时前面只有一个元素，当然是有序的。第二趟比较：将第3个元素插入前面的有序子序列，前面的2个元素是有序的。然后反复执行，第n-1趟比较：将第n个元素插入前面的有序子序列，前面n-1个元素是有序的，最终n个子序列排好序了。

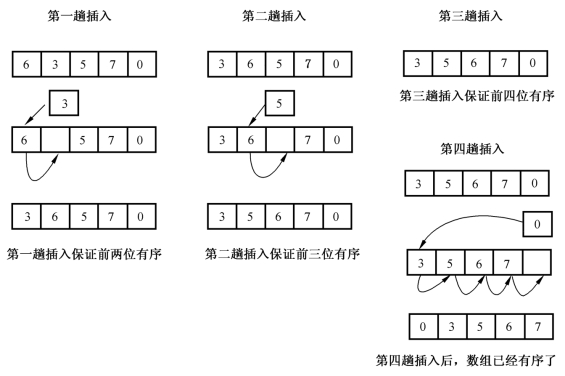
图3-29 插入算法示意图