1.概念和术语

任何专业的学科都有很多专业的基本概念术语，能够更方便地表达专业性的内容，下面我们将对数据结构中的概念和术语赋以确定的含义，以确定与学生取得“共同的语言”。

(1)数据

数据是对客观事物的符号表示，在计算机科学中是指所有能输入到计算机中并被计算机程序处理的符号总称。数据是信息的载体，它能够被计算机识别、存储和加工处理。计算机科学中，所谓数据就是计算机加工处理的对象，它可以是数值数据，也可以是非数值数据，如图像、声音、文本等。表3-2中所有的内容都是数据。

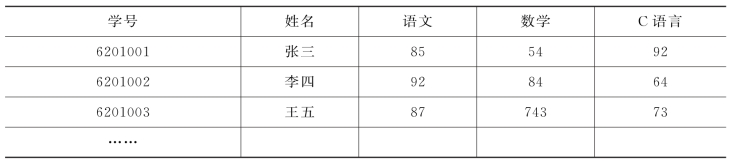
表3-2 学生成绩表

(2)数据项

数据项是数据不可分割的最小单位。数据项有名和值之分，数据项名是数据项的标识，用变量定义，数据项值是数据项可能的一个取值。表3-2中姓名就是数据项，它的取值可以是张三、李四、王五等。

(3)数据元素

数据元素是组成数据的基本单位，在计算机程序中通常作为整体进行考虑和处理。数据元素一般由若干数据项组成。表3-2中学生的基本信息就是一个数据元素，由学号、姓名、语文成绩、数学成绩、C语言成绩等数据项组成。

(4)数据对象

数据对象是具有相同性质的数据元素的集合，是数据的一个子集。表3-2中一个班级的成绩表可以看作一个数据对象。

(5)数据结构

数据结构：相互之间存在一种或者多种特定关系的数据元素的集合。在任何问题中，数据元素都不是孤立的，数据元素和数据元素之间存在着关系，这种数据之间的关系就称为结构。

数据元素和数据元素之间的关系称为结构，相同的数据元素不同的关系构成不同的数据结构。比如说把人看成是数据元素，那么人与人之间的关系有很多种，比如：同学关系、朋友关系、师生关系，进而产生了同学结构、朋友结构、师生结构，所以可以看出数据元素相同的情况下，数据和数据之间关系的不同，那么形成的数据结构也是不同的。

上面所说的数据结构中数据元素的关系描述的是数据元素之间的逻辑关系，因此数据结构称为数据的逻辑结构。然而，我们讨论数据结构是为了在计算机中实现对数据的操作，数据结构在计算机中的表示称为数据的物理结构，又称为存储结构。所以，数据结构从两个角度来看分为数据的逻辑结构和物理结构。

2.逻辑结构

数据的逻辑结构可以看作是从具体问题抽象出来的数学模型，描述的是数据元素之间的逻辑关系。在数据结构这门课程中，根据数据元素之间逻辑关系的不同，通常有下列几种基本逻辑结构：线性结构、树形结构、图状结构。

(1)线性结构

线性结构是最常用、最简单的数据结构，包括线性表、队列、栈等都属于线性结构，线性结构中的数据元素之间存在一对一的关系，每个数据元素有且只有一个前驱(第一个数据元素除外)，每个数据元素有且只有一个后继(最后一个数据元素除外)，如图3-9所示。

图3-9 线性结构

(2)树形结构

树形结构中的数据元素之间存在一对多的关系。比如，一个单位的工作人员之间的关系可以表示成一棵树，每个人只有一个直接领导(单位的最高领导除外)，有多个直接下属(最基层的工作人员除外)，树形结构广泛应用于具有明显层次关系的人类社会的族谱、各种社会机构中，如图3-10所示。

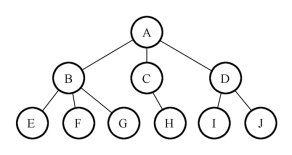
图3-10 树形结构

(3)图状结构

图状结构中任意两个数据元素之间都可能相关，数据元素之间存在多个对多个的关系，图状结构也被称网状结构，铁路交通图是一种典型的图状结构，任意两个城市之间可能存在多条路径连通，图状结构被用于描述各种复杂的数据对象，如通信网络结构、国家之间的外交关系、人与人之间的社会关系等，如图3-11所示。

图3-11 图状结构

使用示意图来画逻辑结构的时候，要注意：每一个数据元素都用一个圆圈来表示。数据元素和数据元素之间的逻辑关系用连线来表示，如果这个逻辑关系是有方向的，那么使用带箭头的连线来表示。

3.物理结构

数据在计算机中的表示称为数据的物理结构或存储结构，它研究数据结构在计算机中的实现方法，包括数据结构中元素的表示及元素间关系的表示。数据的存储结构又可分为顺序存储结构或链式存储结构。

(1)顺序存储结构

把数据元素存放在地址连续的存储单元里，其元素之间的逻辑关系和物理关系是一致的，如果在逻辑上两个数据元素是相邻的，那么在物理内存单元上两个数据元素也一定是相邻的。如图3-12所示，数据元素①和数据元素②在逻辑上是相邻的，同时二者在物理存储器中的地址也是相邻的，满足这种情况的存储结构就叫作顺序存储结构。

图3-12 顺序结构

(2)链式存储结构

把数据元素存放在任意内存的存储单元中，这些存储单元可以连续也可以不连续。元素之间的逻辑关系和物理关系不一致，不能通过物理关系来表示逻辑关系，因此需要一个指针存放数据元素的地址，这样通过地址就可以知道相关联的数据元素的位置，如图3-13所示。

通过图3-13可以发现数据元素在内存中是随意存储的，没有规律，数据元素和数据元素之间的关系通过指针表示，通过看图可以发现数据元素③有一个箭头指向了数据元素④，这个箭头就是指针，通过指针就表示了数据元素③和数据元素④之间的逻辑关系，数据元素③和数据元素④是相邻的，数据元素③的后继是数据元素④，数据元素④的前驱是数据元素③。

图3-13 链式存储

用一种形象的方式来区别一下顺序存储结构和链式存储结构，现在有A、B、C、D四个人，相当于四个数据元素，他们之间是有逻辑关系的，现在要他们进入1、2、3、4四个房间中，就相当于进入4个相邻的内存单元中。

如果要是顺序存储结构，那么A进1，B进2，C进3，D进4，因为A、B、C、D的逻辑关系是紧邻的，所以他们进入的房间也是紧邻的。

如果要是链式存储结构，那么A进2，B进4，C进1，D进3，虽然A、B、C、D的逻辑关系是紧邻的，但是它们并没有按照紧邻的关系进入紧邻的房间。

4.线性表的存储表示和实现

(1)线性表的顺序表示和实现

线性表的顺序表示指的是用一段连续的存储单元依次存储线性表的数据元素。线性表的这种表示方式又称顺序表，线性表(a1，a2，…，a n)的顺序存储结构如图3-14所示。

图3-14 线性表顺序表示

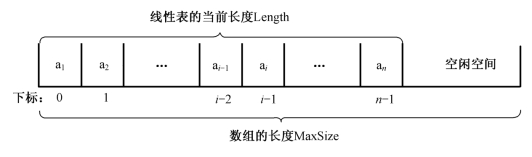
如图3-14所示，a1是这个顺序表中的第一个元素，所以它的标号是1，同理a n是该顺序表中的第n个元素，所以它的标号是n。但是在计算机编程语言中却不是这样，计算机语言规定元素下标从0开始，也就是说a1的标号是0，而a n的标号是n-1，如图3-15所示。

(www.daowen.com)

图3-15 线性表的计算机表示

因为顺序存储是地址连续的，所以只要知道任意一个元素的内存地址，那么就可以，通过公式LOC(a i)=LOC(a1)+(i-1)c获取到所有元素的内存地址，LOC表示地址的意思，LOC(a1)表示数据元素a1的地址，c表示存放一个数据元素的所占的内存空间大小，如图3-16所示。

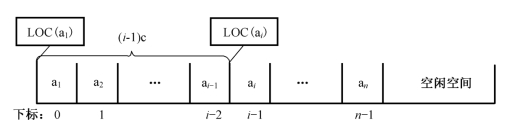
图3-16 线性表地址计算

只要获得线性表中第一个元素的内存地址，那么通过这个公式可以随时获取该线性表中任意一个数据元素，无论数据元素在什么位置，都会使用相同的时间获取到，我们把具有这一特点的结构叫作随机存取结构，这是顺序存储的优点之一。

1)插入操作

顺序存储结构中每个元素都相互挨着，如果要在i位置插入一个数据元素，因为没有空间，所以只能从最后面的元素开始直到第i个元素，都逐渐往后移一个空间，这样i位置就空了，就可以把元素放到这个位置，这样就实现了元素的插入操作。

其实在实际生活中也有类似的情况，当排队买火车票的时候，有一个人说有急事能不能在你前面插个队，这个时候要想让这个人插入进来，不能你先往后移，因为你后面还有人，你一移动肯定是踩到后面人的脚了，所以只能最后一个人往后移一步，倒数第二个人往后移一步，直到你往后移一步，这样就为这个人创造了一个空间，这个人就可以插入到队伍中了，需要注意的是这个人的位置是原来你的位置，你往后移了一步，把你原来的位置给他了，如图3-17所示。

图3-17 插入操作

2)删除操作

因为顺序存储结构的每个元素都是挨着的，假如删除第i个元素，那么第i个元素的位置就空了，第i-1个元素和第i+1个元素就不挨着了，这显然不符合线性表的定义，所以为了解决这个问题，从第i+1个元素开始到最后一个元素，都依次往前移一个空间，这样就会使得第i-1个元素的后继是第i+1个元素，第i+1个元素的前驱是第i-1个元素。

还拿买火车票举例，排队买火车票的时候，经常有人排着队就突然离开了，这个时候他原来的位置就空了，那么他后面的那个人会往前一步，占据他的位置，之面的也会跟上，直到最后一个人，那么这个就类似删除操作，如图3-18所示。

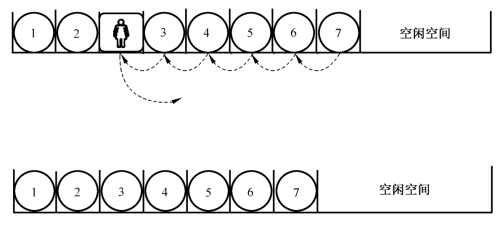
图3-18 删除操作

(2)线性表的链式表示和实现

在谍战剧中经常有人在敌方系统内潜伏，为了保证安全，他们往往单线联系，就算敌人抓住其中一个，也不能在很短时间抓到所有的人，因为每个人只能找到唯一的上级和唯一的下级，这种潜伏系统特别像线性表的链式存储结构。

链式存储结构是线性表在计算机中的另外一种表示方法，由于它不要求逻辑上相邻的元素在物理位置上也相邻，因此它可以解决顺序存储的大量移动元素的问题。

线性表的链式存储结构的特点是用一组任意的存储单元存储线性表的数据元素(存储单元可以连续也可以不连续)，对于每一个数据元素a i结点来说，除了存储其本身的信息之外，还需要存储直接后继的信息(直接后继的地址)。存储结点数据信息的域称为数据域，存储直接后继结点位置的域称为指针域，指针域中存储的信息称为指针。n个结点连接成一个链表，即为线性表(a1，a2，…，a n)的链式存储结构。

如图3-19所示，结点a i和结点a i+1在物理位置并没有紧邻在一起，然而结点a i的指针域存储0500，正好是结点a i+1的内存地址，所以结点a i的后继就是a i+1结点，这样虽然结点a i和结点a i+1在物理上不相邻，但通过指针，结点a i和结点a i+1在逻辑上已经相邻。

图3-19 线性表链式表示

如图3-20所示，p是指向线性表中结点a i的指针，则p→next是指向结点a i+1的指针。换句话说，若p→data=a i，则p→next→data=a i+1。

图3-20 插入操作后链表结构

在单链表中，要想取得第i个数据元素必须从头指针(指向第一个结点的指针)出发寻找，因此，单链表是非随机存储结构，所以它查找速度非常慢。

1)插入操作

如图3-21所示，插入操作是将值为e的新结点插入到单链表的第i+1个位置上。首先找到待插入位置的前驱结点，即第i个结点，再在其后插入新结点。

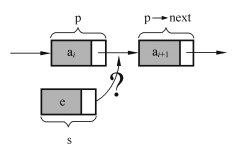
图3-21 插入操作前链表结构

假设第i个结点为p，首先令新结点s的指针域指向p的后继结点a i+1，再令结点p的指针域指向新的插入结点s，这样就实现了结点的插入操作，实现插入结点的代码片段如下：

s→next=p→next；

p→next=s；

这两句代码就完成了链表的插入操作，插入过程如图3-22所示。

图3-22 插入操作后链表结构

插入操作就像甲、丙同学手拉手上学，路过乙同学家，乙同学也加入他们中间，此时甲同学和丙同学手分开，然后乙拉上丙同学的手，而甲拉上乙同学的手，他们三个手拉手地去上学了，如图3-23所示。

图3-23 插入操作实例图

2)删除操作

在单链表中删除元素a i时，其实是在单链表中实现元素a i-1、a i和a i+1之间的逻辑关系的变化。先找到单链表中的第i-1个结点，即被删结点的前驱结点，然后令第i-1个结点的指针指向第i+1个结点，这样就将结点a i从链表中删除了。其操作过程如图3-24所示。

图3-24 删除操作

实现删除结点的代码片段如下：

q=p→next； //令q指向被删除结点

p→next=q→next；//将*q结点从链中断开

free(q)；//释放结点的存储空间

假设结点p为找到的被删结点的前驱结点，为了实现这一操作后的逻辑关系的变化，仅需要修改p的指针域，即将p的指针域next指向q的下一结点。

删除操作就像甲、乙、丙三个同学手拉手放学回家，走着走着，乙同学到家了，此时乙同学松开甲、丙的手，而此时甲同学和丙同学拉起了手，一起继续往前走，如图3-25所示。

图3-25 删除操作实例图