（1）数学也是开始！（第一学期微分法）

关于喜欢数学还是讨厌数学的变化调查表（和会否没有关系）：

①很喜欢，②喜欢，③一般，④讨厌，⑤很讨厌。

表15　中里百合子的统计数据

期望：这一年是我高中数学生涯的最后一年，所以我要努力学习。

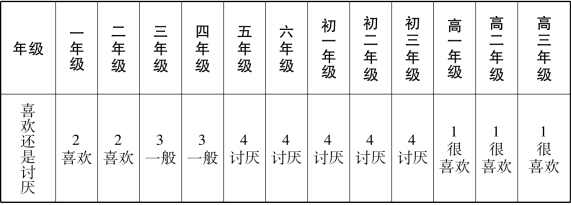
表16　石田麻里的统计数据

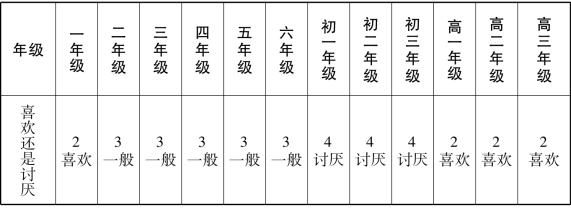
期望：我想每天都朝着目标一步一步脚踏实地地努力前进。

表17　田代郁子的统计数据

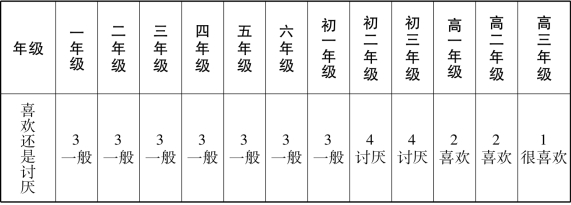
期望：之后考上短大的话，就没有数学可以学了，所以现在要努力学习数学。

（2）从“山路”到“高速公路”

一开始听说是微分法，感觉非常困难，但是因为老师是用从“山路”逐渐到“高速公路”这样循序渐进的方法来教授的，所以我可以理解得很透彻。我惊讶地发现，居然有那么多方法可以寻找瞬间的速度。尤其是这个微分法，一下子就可以求出导函数，一下子就可以求出瞬间速度。

这就是“超级除法”。我们第一次做的那个容积最大的盒子的答案到底是什么？在目前这个阶段还求不出来吧？不过不管怎样，我很高兴我了解了微分法。虽然今后可能会遇到更难的问题，但是我会努力的。

（3）给北海道的美咲的信——今天做了容积最大的盒子

参见第五章第三节。(www.daowen.com)

图34　折纸实验

（4）按重量计算面积的实验感想（第二学期积分法学习）

x的值越小，斜线部分就越重。如果裁得好的话，全部就都能变成一样的。因为纸很硬，所以用剪刀剪很困难，结果有点偏离了。下次再做的话，我想我会做得更好。

表18　重量实验的结果（有误差）

（□长方形的更重，◎恰当，△斜线部的更重）

其他学生的感想：“在y=x2的图像中，我们发现斜线部分的面积总是长方形面积的1/3。起初，3张斜线的一边看起来更重，但重量其实是一样的。我检查了一下剩下的部分，也还是一样的。”（小N）

表19　重量实验的结果

（□长方形的更重，◎恰当，△斜线部的更重）

注意：在y=x2的图像中，如果我们能够发现斜线部分的面积总是长方形面积的1/3这一性质，那么利用这一性质，我们就可以很容易地计算出斜线部分的面积，从而得出一个定积分公式。∫0x2dx=［1/3x3］10的x3前面的1/3表示的就是长方形面积的1/3。（参见第五章第四节。）

（5）转动抛物线陀螺（参见第四章第二节）

要想转动5个陀螺的话，重心的计算非常困难。但是我试着在重心的位置上钻了个洞，试了一下后就很顺利地转起来了，我太高兴了。之后，我还涂了颜色，2种颜色混合在一起，线条变成圆圈，非常漂亮。

第三学期的毕业论文等问题，将在之后的第三节中举例说明。