以本质为重的学习，在第二学期就是重视积分本质的学习，积分的本质就是将已经被细致分解开的事物再次连接组合起来。使用这个方法，来求出被曲线所围成的图形的面积，继而推导出积分公式。首先我们来求出抛物线y=x2坐标图所围成的图形的面积。

抛物线：y=x2的曲线与坐标轴围成的图形的面积

画出y=x2的图，求x的值为0到1之间的部分的面积。

（1）y=x2的图如下所示，分成了10级“楼梯”，求各个长方形面积的总和。

图23　y=x2的图像分为10级“楼梯”

表13　10级“楼梯”各长方形的面积总和

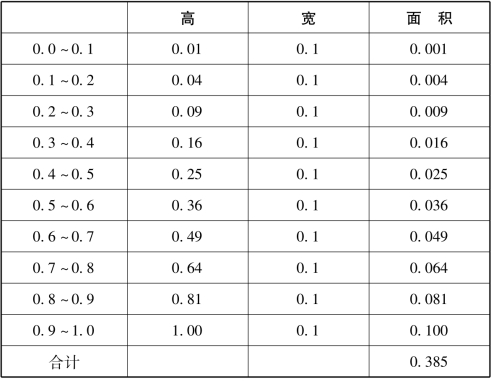
（2）用同样的方法来计算100级“楼梯”的面积。

表14　100级“楼梯”各长方形的面积总和(www.daowen.com)

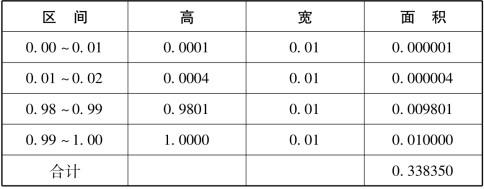
100级“楼梯”图形的面积总和为0.338350。

（3）1000级“楼梯”面积的总和为0.333833500。

（4）10000级“楼梯”面积的总和为0.333383335000。

……

（5）类推下去，被无限细分的楼梯图形的面积就应该为0.33333 3……用分数表示的话，就是1/3，即斜线部分的面积为1/3。

上文中的图23表示的是，将y=x2所包含的面积从0到1的区间分成10个长方形，分别用（长×宽）求出面积，并将其相加。

长方形是从图中抽出来的一部分，因为存在误差，所以要将其缩小，再进一步细分就好了。（4）是根据（1）（2）（3）的结果预测的变成10000级“楼梯”的情况。

进而，如果想象从0到1的区间无限细分的情况，误差会消失，所以长方形的总面积即被曲线围成的图形的面积。这个面积是0.333……用分数表示是1/3。