1979年第一学期的第一节课上，我带着“微分入门”教材和写着“用折纸制作容积最大的盒子”的纸以及折纸去了教室。在打印的纸张上，写着“凭直觉制作容积最大的盒子”，以及“第一学期，用微分法计算出最大的盒子并制作”这样的内容让学生来明白需要达到的目标。

图11　凭直觉制作容积最大的盒子

之后，我以这样形式开始了一个学期的微分课程，几个月后，终于在7月迎来了计算并制作最大容积的盒子的日子。

先让学生做，然后让学生把计算后制作的盒子和最初凭直觉制作的盒子进行对比，并让学生自己检查一个学期的学习成果。最后，在黑板上粘贴的纸上画上大的图表，并在每隔5毫米的地方贴上同学们折的14个盒子。

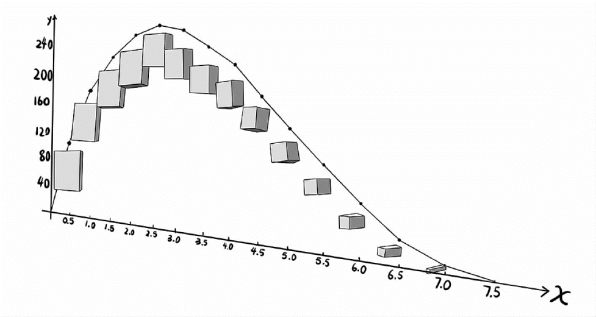
图12　折纸制作的大小不同的盒子

这样一来，不同的折叠方法会折出什么样的盒子就一目了然了。从扁平的盒子到尖尖的盒子，不仅仅是量的变化，而且盒子的形状也随着折叠方式的改变发生了令人惊喜的变化。特别当我把切下了边长为7厘米的正方形后制作成的尖尖的盒子贴上黑板时，教室里一下子就响起了开心的笑声。

在这些盒子中，我们发现折成的边长为2.5厘米的正方形盒子的容积是最大的。实际的动手操作在课堂上产生了一种光靠计算无法体味的快乐。这说明如果能从关联中去把握事物的话，理解方式就会发生很大的变化，学习也就有了乐趣。看到贴在黑板上的盒子，学生小K还作了一首诗。

像闪烁的星星一样（小K）

细长的盒子，

扁平的盒子，

各种各样的盒子。

即使看起来是最大的，

但实际上并不大。

觉得小的东西，

却意外地很大。

总觉得在宇宙的彼岸，(www.daowen.com)

闪耀的星星，

它们看起来又大又小，

它们看起来又小又大。

我们所居住的世界，

为什么净是些让人搞不懂的事情呢？

但是正因为如此，

才让人快乐，不是吗？

即使用同样的东西制作，

即使只有一点点不同，

也会有所不同，

即使是同样的折纸。

稍微动点脑筋，真神奇。

即使出生在同样的星球上，

为什么会如此不同呢？

我也不知道。

虽然实践课程只用了2张折纸，但结果不仅让课堂的气氛一下子就活跃起来了，还诞生了“折纸诗”，这让我感到非常惊讶。