1998年，我再次教授一年级2个班的数学I（4学分）。在第三学期的概率课上，我开展了第二次关于核电站的课。开始上课时，我一时兴起，用“核能委员会”提出的10-9的概率，试着计算了世界上500座核电站发生重大事故的概率，结果得出100年内至少发生1次重大事故的概率只有1/10000这个低数值。看见这个数字，我也不由自主地发出了“啊——”的惊叹。在这里，我产生了一个很大的疑问，这难道是为了解释核电站“安全神话”而被滥用的概率吗？

10-9的假说是为了说明世界上的核电站即使在100年内也不会发生1次重大事故而倒推得出来的数字。

由于已经发生了2次重大事故，美国核能委员会的10-9这一数字很快就露出了破绽，这会不会是套用概率，用科学来伪装核电站的“安全神话”呢？因此，在第二次课上，作为一种新的尝试，我想把目光转向这种假说所具有的问题上面来。我想，如果在课堂上验证10-9的假说应该会很有趣吧。

为此，我们必须亲自来确认这个10-9的假说会产生什么样的结果。我想从结果出发，发挥学生的想象力，来推测为什么会出现这样的假说，并进行讨论。因此，我决定准备教学资料，让大家根据这2种假说，分别计算60年内至少发生1次重大事故的概率。

在第二次上课之前，我从学生手上的现代社会资料集中选出要点并打印出来，让学生对核电站进行基础性的学习，另外，还配合《切尔诺贝利事故发生12年——与癌症作斗争的孩子们》（埼玉报纸1998年2月15日）的报刊内容让学生进行补充阅读。并在让学生们了解了在14岁因甲状腺癌而去世的名为“坦尼亚”的少女的悲惨故事后，才开始进入计算的学习。然而，使用2种假说的计算却导致了意外的混乱结果。

核电站的安全性？查验2种假说（用12进位的电子计算器）

假说1：一座核电站在一年发生重大事故的概率仅为10-9，绝对安全！［美国核能委员会的假说（1974—1975年）］

表10　美国核能委员会的假说

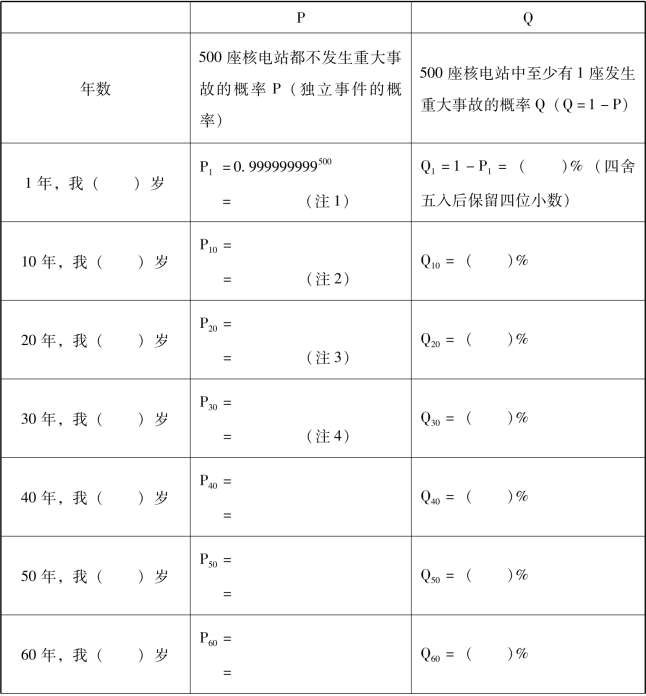
续表

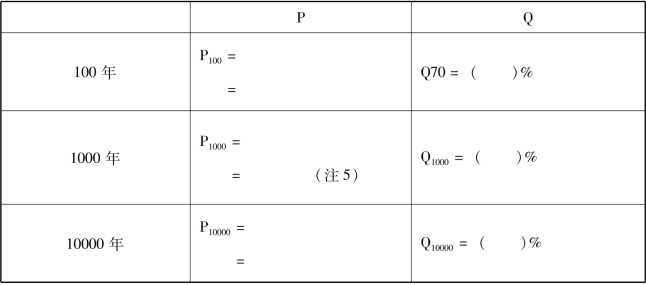
指数计算：32×34=32+4=36 34×34=（34）2=38
320=（34）5，用计算器计算出来的结果就为3486784401
跟直接算320相比，用（34）5来结算更为简便。
注1：①因为1年内发生重大事故的概率为10-9，所以不发生重大事故的概率就
为0.999999999。
②500座核电站一年不发生重大事故的概率为0.999999999500=
［（0.99999999910）10］5
注2：P10=（P1）10
注3：P20=（P10）2
注4：P30=（P10）3
注5：P1000=（P100）10(www.daowen.com)

假说2：1座核电站1年内发生重大事故的概率大概为1/10000［科学家同盟的假说（1975年）］

注：1975年后发生重大事故的概率，基本和推测的结果是一致的。400座核电站在50年运行期间，发生了2次重大事故。

表11　科学家同盟的假说

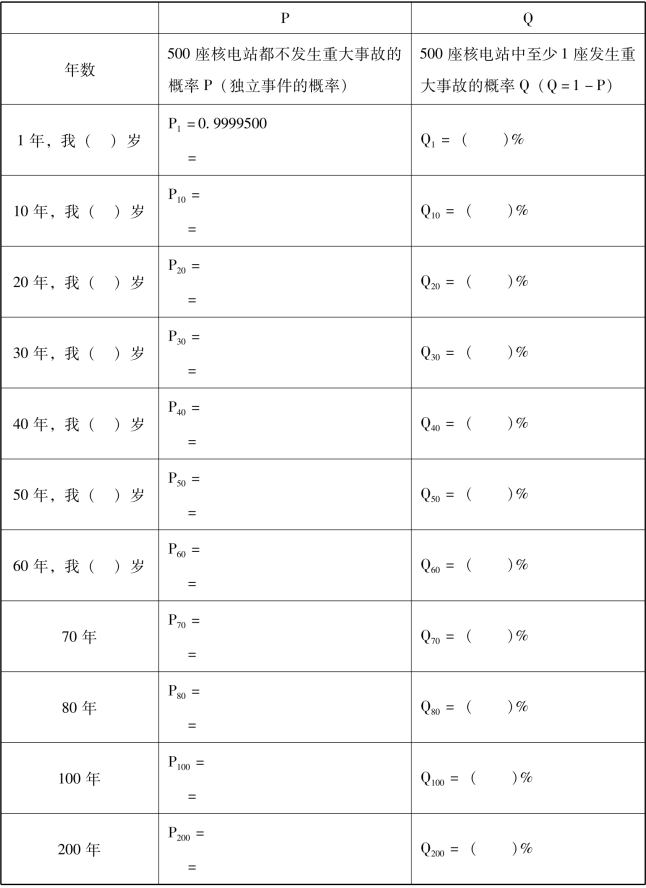
根据2种假说分别计算出了核电站发生重大事故的不同概率，请谈谈你对该结果的看法。

关于本课程的感想：

世界上的核电站反应堆在60年内至少发生1次重大事故的概率

假说1：假设1座核电站的反应堆在1年内发生重大事故的概率为1/1000000，60年内至少发生1次重大事故的概率为0.30%。

假说2：假设1座核电站的反应堆在1年内发生重大事故的概率为1/10000，60年内至少发生1次重大事故的概率为95.03%。

表12　学生对以上结论的看法