不祥的预言：没想到在我们有生之年，核电站发生重大事故的概率居然高达约92%！

我决定在1997年一年级2个班第三学期的概率课上把“核电的功过”这一尚未解决的热点问题作为主题来开展教学。这堂课上出现赞成、反对2个立场，包含可以进行讨论的要素。在课堂上，首先，为了获得关于核电站的基本知识，学生要活用手头的现代社会资料集，事先学习到现在为止发生的重大事故、日本的核电站的状况以及“死之灰”等放射性废弃物等内容。

其次，根据藤村老师的报告，核电站发生重大事故的概率是在“从今往后10年”的期间内算出来的33%这个结果。但是“33%”这个数字应该怎么考虑才好呢？因为是一个比较难判断的数字，所以我们试着探讨了一下有没有得出更明确数字的可能性。对于高中一年级的学生来说，50年后就是66岁了，在自己有生之年是否会发生核电站重大事故这样的问题，想想都觉得很有趣。核电站的数量，因为据说在建设中的就有100座左右，因此为了计算的简单化，就假定全世界总共有500座核电站。

计算方法是用和求掷骰子2次，至少出现1次1的概率的问题一样的解法（可以按“余事象”定理求出，计算方法如下）。

投掷2次骰子时，至少投出1次为1的概率的计算方法

出现1的情况打√ 出现1以外的情况打×

至少出现一次1的情况：请参照下表。

表9　投掷2次骰子至少投出1次1的概率

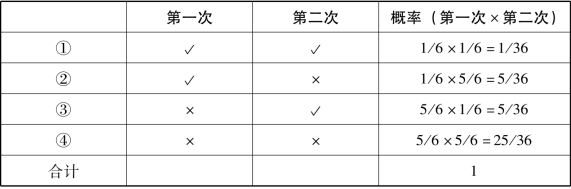
至少掷出1次1的概率为：①+②+③=11/36…………（1）

2次都不会是1的概率：④=25/36…………（2）

“余事象”定理：按照①②③④相加后得出1的概率的特质，至少一次投出1的概率就不是①②③的合计，而应该是1-④得出的结果。

所以，至少一次投出1的概率就应该是1-④=1-25/36=11/36。这和（1）的答案也是相同的。(www.daowen.com)

随着投掷次数增加为3次、4次、5次、6次，投掷的可能性就会变成8种、16种、32种、64种，“余事象”定理的计算方式在这里发挥了巨大的作用。在核电站发生核泄漏的问题上，我们也可以用假定投掷500次骰子的情况来进行考虑。

1座核电站在1年内发生重大事故的概率为1/10000，正好相当于掷骰子点数为1的概率为1/6的情况，不发生事故的概率为9999/10000，相当于点数不为1的概率为5/6的情况。

计算世界上500座核电站1年内发生重大事故的概率时，如果把500座核电站的情况全部列举出来的话，数量就会变得很庞大，怎么也计算不出来，但是使用“余事象”（某个事物完全不会出现的情况）定理的话就可以得出一个结论，也就是说，用1减去完全不会发生事故的概率，就能得出结果。

如果使用电脑进行这个计算的话，50年内至少发生一次重大事故的概率为92%。乍看之下，1/10000的概率往往被误认为是“1万年内只可能发生1次重大事故，所以不会轻易发生重大事故”，但是如果按照“500座核电站50年内至少会发生1次重大事故的概率”来计算的话，就会出现很严峻的数值。这就是这个计算的有趣之处。把世界上所有的核电站作为对象，是因为不管哪个国家的核电站发生了重大事故，都会对整个地球造成严重的破坏和污染。

世界上500座核电站在50年内至少发生1次重大事故的概率

首先我们假定1座核电站1年内发生1次重大事故的概率为1/10000，那么不发生重大事故的概率则为：1-1/10000=9999/10000=0.9999

500座核电站1年内不发生重大事故的概率为：0.9999500=0.9512

500座核电站在50年内不发生重大事故的概率为：0.951250≈0.0820

因此，500座核电站50年内至少发生1次重大事故的概率为：1-0.0820=0.9180=91.80%

那么，根据天气预报所说，明天的降雨概率为92%的话该怎么办呢？一般人为了慎重起见，会带把折叠伞出门吧。或者是因为不过是概率，下不下雨都不知道而无视这92%的概率，不带雨具就出门呢？人们接受这种天气预报概率的想法和接受核电站重大事故发生的概率的想法其实是一样的。学生自己通过计算得出了在之后的50年内，有约91.8%的概率至少会发生1次核电站重大事故这样不吉利的预言。

这个计算结果给学生带来了巨大的冲击。那“核电的功过”问题就成为了每个同学不能漠视的一种存在。