指数函数是指在一定的时间或期间内，以一定的倍率递增的函数。在栗子包的情况中，一定的时间是5分钟，一定的倍率是2倍。小K想出的库勒的倍率则是4倍。

那么，假设我们看见小额房贷的信息，写着年利率20%，借1万日元，1年的利息就是1万日元×0.2=0.2万日元，加上本金的话是1.2万日元，与最初的1万日元相比是1.2倍。

如果按照20%的复利计算利息的话，那就是倍率为1.2倍的指数函数。指数函数的特征是呈现暴发性的增长。那么，1.2倍的倍率真的会产生让人吃惊的变化吗？

每年增加1.2倍，5年之后会增加多少倍？要得出结果，我们把1.2重复5次即可。如果使用计算器的话，计算起来非常简单，大约是2.5倍。借100万日元的话，等于要还250万日元。

但是实际的偿还方法是从借钱的第二个月开始以本金等息的形式来每月偿还，因此实际的偿还额不会是250万日元。

我在网上查了一下“本金等息支付”。输入借入金额（100万日元）、年利率（20%）和付款次数（60次），按下“计算”键，计算结果马上就会出现：每月的还款额为26494日元，总支付金额约为1596800日元。

计算器的使用方法

1.22的计算 普通计算法1.2×1.2=1.44

例1 1.22的计算 按1.2××=（按1次“=”）可以得到答案1.44

例2 1.23的计算 按1.2××==（按2次“=”）可以得到答案1.728

例3 1.24的计算 按1.2××===（按3次“=”）可以得到答案2.0736

以此类推，多按1次=就相当于多乘1次，用这样的方式可以计算5次方、6次方等

但在研究小额放贷的利息时，我们很难对本金等息支付的方式进行研究。因此，让我们先单纯地计算本金和利息合计会变成几倍，再来进行比较研究吧。

因为小额放贷的广告很有意思，所以我决定调查一下不同的利息会让借款额变成原来的几倍？在复利计算中，这样想就好了：如果利息是20%，1年就能增加1.2倍，如果是15%，1年就能增加1.15倍。在此，我们先来回顾一下在修改《利息限制法》之前的20世纪80年代A公司的广告吧。

现在，《利息限制法》规定的利率上限是20%（无罚款规定），出资法的利率上限是29.2%（有罚款规定）。但是，在网上调查高利贷利率的结果显示，26家公司中有21家公司的利率都超过了《利息限制法》的规定，其中10家公司都达到了出资法上限的29.2%，在《利息限制法》规定的20%以下的只有5家。

那么，在上面的广告（《出资法》及《利息限制法》修正前的广告）中的各种借款方案中，本息合计一次性支付的话，我们来看看在出台法律修正案以前，还款的时候金额会变成原来的几倍吧（使用计算器，参见表3）。(www.daowen.com)

表3　法律修正案出台前的还款金额

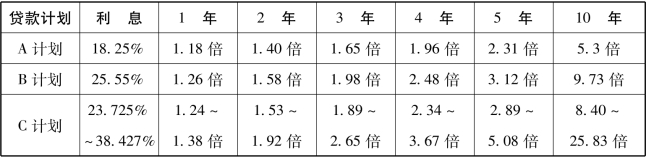
在上述“现金贷款”的例子中，利息为38.427%的话，（《出资法》修正之前）如果借50万日元，5年时间就会翻5倍，需要偿还250万日元，并且这种情况是被允许的。而且如果借10年的话，就需要偿还高达25倍的借款金额。

1998年9月，研究该小额放贷广告的学生们发表了以下感想。

“虽然看到这样的现金贷款广告，觉得贷款很方便，但是这次的课让我明白了，走错一步就会出大事，所以我绝对不会借的。”（小T）

“我明白了这些甜言蜜语是有内幕的，不要上当。”（小H）

“在例题中，以10%的利息来计算的时候，我就已经觉得2.5倍的利息很高了，没想到现金贷款的利息是它的10倍，简直高得离谱。”（小Y）

“如果是我的话，我不会接这样的广告（广告中有演员M的笑脸）。不是为了帮助缺钱的人而放贷，而是利用这个机会来谋取利益，这简直让人不能容忍。”

“我希望（演员M）在知道这是一家什么样的公司的前提下再决定要不要给他们拍广告。”（小A）

“我觉得10年间这么多的利息有点太高了，不能随便打电话去借钱。”（小S）

“随着还款期限的延长，会变成一笔大额的还款，这一点我是知道的。但是按年利率计算的话，10年后的还款额比我想象的还要多得多，这让我很吃惊。”（小Y）

小额放贷已经成为一个很大的社会问题。在经济不景气的情况下，小额放贷危害在不断增加，光在2004年，申请破产的案件就达到了21万件。而且在今后，大型银行中有安装“银行和小额放贷共用申请机”的倾向，关于小额贷款的电视广告也开始大量出现，所以使用银行的人更容易去进行小额借款。在这样的社会背景下，对小额放贷问题的学习是非常必要的。

小额放贷的研究是关于在一定期间内以一定倍率变化的倍数变化的代表性例子，是了解数学与现实世界之间密切联系的很好的教材。学生们可以通过将含糊的利息改为5年、10年等一定期限的倍率进行比较，来了解如果借小额贷款会发生什么情况。在这里，学生们发现了仅靠四则运算看不到的呈暴发性增加的成倍变化的新世界。

注：小额放贷（消费者金融）的利息一般只对本金进行单利计算，但非法“黑市金融（即高利贷）”的利息则是复利计算。在本节中，我们只是使用小额放贷广告中出现的利息，在假定是复利计算的情况下，单纯计算还款额会成为借款额几倍的情况。