作者藤子不二雄先生知道，如果使用“膨胀剂”的话，就会从1个增加到2个，从2个增加到4个，即每5分钟增加一倍。那么1小时后是4096个，2小时后是16777216个，再过15分钟后就会超过1亿个，一天之后地球就会被栗子包淹没。

所以哆啦A梦对用这种药犹豫不决，并让大雄答应“要全部吃完”。但是，问题发生后，哆啦A梦企图让火箭载满栗子包飞往宇宙另一端的做法又会有什么后果呢？那些栗子包以同样的势头分裂并继续增加的话会怎么样呢？需要多长时间栗子包会填满整个宇宙呢？使用“膨胀剂”的课程由此进入思考栗子包后续的正题部分。

要想考虑这个问题，就必须计算宇宙的大小和膨胀的栗子包的体积，再进行比较。

在开始计算这个题之前，学生们有什么样的预测？让学生试着举手发言后，发现2年级4个班级里举手回答的162名学生中，回答“1天后”的学生只有2人，回答“1个月后”后的有18人，回答“1年后”的有69人，回答“10年后”的有50人，回答“100年后”的有18人，回答“1万年后”的有3人，回答“1亿年后”的有2人。

几乎所有的学生都没有想到，仅1天时间，栗子包就会暴增并填满整个宇宙。

假设宇宙是一个半径为100亿光年（据说最近学者们认为是138亿光年）的球体，计算它的体积大小；假设1个栗子包的体积为100立方厘米，在这样的前提条件下如果把1天后栗子包的个数拿出来比较，就会得出：1天后的栗子包个数比进入宇宙时的栗子包的个数还要多400倍这样一个惊人的结果。

表1　什么时候栗子包会把宇宙填满？

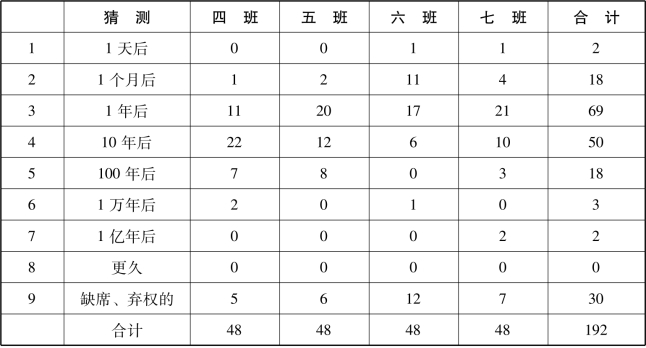
就连这个被认为无限大的宇宙也会在1天之内被栗子包轻松填满。我们认为“宇宙无限大”的常识被栗子包轻而易举地打破了。

宇宙的大小和栗子包的个数（计算结果）：(www.daowen.com)

进入半径为100亿光年的宇宙的栗子包的数量　1083个……①

1天后栗子包的数量　4×1085……②

对比①和②，②的数量增加了400倍。

开始时1个变2个，2个变4个，不是什么大不了的增加，但是不久之后，就会出现1亿个在5分钟后变成2亿个的现象。学习指数函数的目的之一就是要抓住这个倍增变化的厉害之处。

指数函数推翻了什么都用比例来看待变化的看法，并让我们得到了“一副新眼镜”，这个“眼镜”可以分辨在自然和社会中成倍变化的事物。指数函数就是解读成倍变化的世界的“眼镜”。

哆啦A梦的错误计算使他担心在1天后，地球会被埋在栗子包底下，但又深信即使栗子包有再强的暴发性增长，也绝对不可能填满这个无限广阔的宇宙。所以他想如果把剩下的栗子包装在火箭上扔到宇宙就放心了。

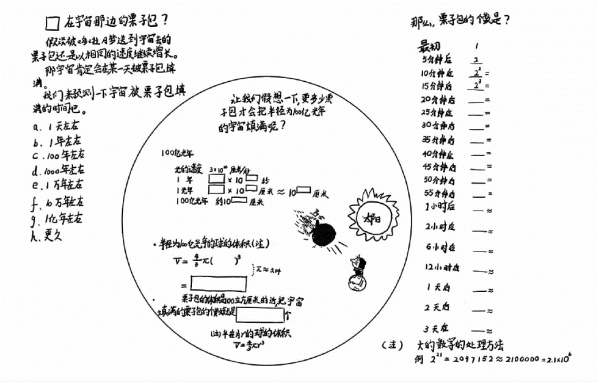
图3　宇宙和栗子包

如果作者对宇宙和栗子包进行过比较计算的话，就不会发生这样的错误计算，结局也会完全不同吧。