（一）内容演示功能

当前国内中高职数学教师使用最广泛的内容演示软件为Power Point，简称PPT，把讲授的内容放入幻灯片中展示，外加音乐、动画、图片、艺术字等。虽说PPT比较简单易用，相对传统教学来说也有明显的优势，但作为一款普适软件，对数学学科缺乏针对性。

Maple和PPT一样能为教师提供操作便捷的技术文件界面，在单个文件中能集成图形、动画、文字、视频等内容，也拥有跟PPT类似的幻灯演示界面。但二者又有本质的不同。

1.数学公式输入

PPT输入数学公式不方便，需要外嵌公式编辑器进行公式输入，操作麻烦，耗费时间较久。Maple能独立键入手写样式的数学符号和公式，或者借助左侧的公式模板进行点选输入，方便快捷。

2.文档层次结构

PPT文档是分页设置的，所有内容不能呈现在一页文档中，看不到文档的主体结构，缺乏层次性。Maple可以将文档按照内容的层次以章节的方式组织在一页文档中，每一节可以通过左端的三角形按钮展开及隐藏，这样可以使用户能够按照任意层次显示文档，使大量内容整合在一个文件中，显得条理分明、层次清楚。

3.演示界面

PPT仅为固化的演示界面，解题过程是静态的，无法根据课堂需要对它进行调整，不利于学生思维的拓展和进行数学探究。Maple为实时动态的演示界面，界面上集成的动画、绘图、运算、电子表格都是以动态的形式存在。教师根据课堂的需求随意调整参数，能即时生成一个新的演示文档。总结以上几点，绘制PPT与Maple的内容演示功能对比如表5-2所示。

表5-2　内容演示功能对比表

续表

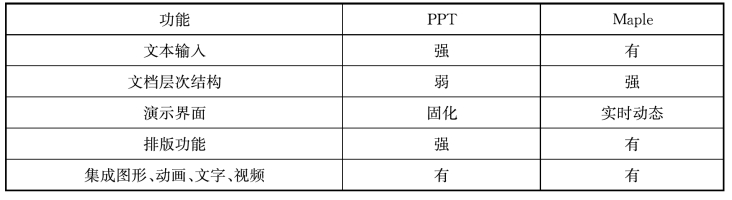
由上表可知，PPT在文本录入、排版功能上强于Maple，但Maple在公式编辑、文档层次、演示界面上比PPT要优越。

综上所述，Maple的内容演示功能更适合数学学科。PPT软件的开发是面向各个学科领域，为了更大限度地赢得用户它会将各个学科偏重率降到最低，无法深入学科内部，无法专为某个学科服务。而Maple软件是一款强大的、专为数学学科服务的软件平台，其专业性和针对性是PPT这种普适软件无法比拟的。

（二）图形化功能

目前高职课堂中使用广泛的绘图软件是几何画板，在课堂上应用它体现以形助数，数形结合的思想方法，深受广大数学教师喜爱。但是几何画板在绘制函数图象上存在一些弱点。下面比较几何画板和Maple的函数绘图功能。

1.绘制函数图象的范围

几何画板绘制函数图象的范围比较有限，能够绘制的函数数量较少。例如它只能绘制以10为底的log常用对数函数和In自然对数函数，不能直接绘制任意底数的对数函数的图象，需要在几何画板中通过换底公式转换后才能绘制。Maple具有庞大的函数库，提供了2000多种数学函数，绘图范围极其广泛。

2.绘制函数图象过程

使用几何画板绘制函数图象需要一定的技巧，它不提供命令行界面直接输入，需要对各个菜单进行多次点选设置函数及参数范围。例如绘制y=sinx，x∈［0，2π］的图象需要如下操作。首先在菜单栏中打开“新建函数”对话框；然后在此对话框中输入函数解析式，点击“确定”按钮，回到主页面；接着再进入“新建参数”对话框，对左区间参数进行点选，返回主界面；再次进入“新建参数”对话框，对右区间参数进行点选，返回主界面；最后依次单击函数解析式，左区间，右区间即可完成绘图，如图5-12所示。这一过程比较麻烦，耗时较久。除此之外，由于几何画板不支持符号运算，因此当区间参数中含有π时，都只会以3.14近似值的方式出现，不利于学生的直观理解。

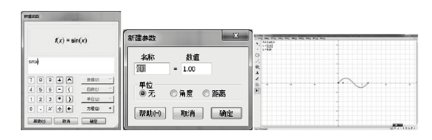
图5-12　函数图象绘制

Maple绘制图象过程：Maple可以通过命令行绘图，只需一个简单的plot（绘图）命令即可绘制图象。而且plot命令中的函数解析式与数学表达式几乎一致，类似手写。一般模式为：plot（函数式，坐标范围，选项），选项可以缺省。例如：绘制正弦函数y=sinx，x∈［0，2π］的图象。在Maple界面输入命令为：plot（sin（x），x=0..2*Pi）；按回车即可绘制图象，如图5-13所示。

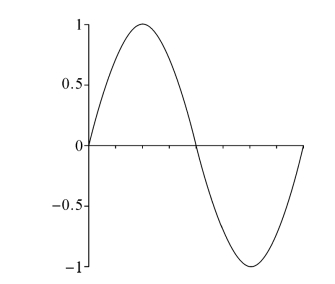
图5-13　正弦函数y=sinx，x∈［0，2π］的图象

由以上可以看出，Maple绘图相当简单，操作快捷，而且支持多种操作即使是对语法命令完全不懂的人，也可以通过点击左侧的面板选择函数解析式，再右击选择上下文菜单中的plot选项即可绘制图象。(www.daowen.com)

3.动画功能

几何画板的函数动画制作需要一定的技巧性，跟它的绘图一样，在制作函数动画时，也需要数次新建函数、新建参数等对话框进行点选。还需要设置多个动作按钮对它的播放进程及返回进行手动控制。制作的过程较为繁琐，需要一定的时间和精力才能完成。

Maple的动画制作非常简单，它的编写原理类似放映电影：将一段时间内的图片一页页的展示。因此在animate（动画）命令中，绘制出函数的图象，再将要变化的参数设置一定的范围即可。一般模式为

animate（plot，［函数式，坐标范围］，参数范围）。

例如，指数函数的动画命令如下

animate（plot，［ax，x=3..3，y=1..10｝，a=2..8｝。

回车即可生成动画，展示底数a从2到8这一区间内指数函数的图象变化情况。Maple会自动生成一个动画播放进度条来设置播放快慢、开始、暂停、前进和后退等功能。还可以手动拖动播放进度条随意观看任何参数值时的图象状态。除此之外，Maple软件内置了许多交互式动画，并按照应用领域归类，方便教师和学生直接调用。

总结以上几点，绘制几何画板与Maple的图形化功能对比如表5-3所示。

表5-3　图形化功能对比表

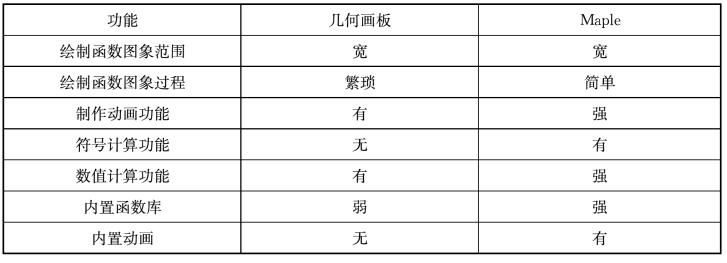
由上表可知，与几何画板相比，Maple绘制函数图象的范围更广泛，绘图和制作动画更为简单方便。同时它的符号计算功能强大，能够将参数值以精确值的形式表现出来，有利于学生直观分析图象。

综上所述，Maple在函数的图形化功能上要比几何画板更优越。Maple操作快捷，绘图和动画功能强大，能生动直观的展示抽象难懂的数学定义和定理。在Maple的支持下，抽象的公式定理也能动起来。在直观地视觉刺激下，学生能迅速找到图形中蕴含的本质规律。这种信息技术辅助下的数形结合的思想方法比起只注重数学推理论证的传统数学要容易和有趣得多。

（三）运算功能

数学课堂中，无论是概念的推理过程，还是讲述习题的过程，都充斥着大量繁杂的运算。教师和学生需要花费许多精力、时间在这些“体力劳动”上。目前高职普遍应用的是科学计算器，但是科学计算器只能支持数值计算，不支持符号计算，但很多数学过程、公式推理都需要符号计算的支持。

Maple除了具有高精度数值计算功能外，还具有无误差的符号计算功能，能处理各种各样繁琐的数学运算。函数调用相当简单，“一键”即可解决复杂的运算问题。让教师和学生可以将繁琐的手工劳动赋予信息技术，将更多的精力放在数学方法和数学思想的掌握上来。

符号计算系统的最基本功能是处理符号表达式，多项式则是最基本的符号表达式。Maple可以用各种方式处理多项式运算。如expand展开、factor因式分解、collect合并同类项和simplify化简等等。调用Maple中的solve函数能“一键”求解不等式（组）或方程（组）。除此之外，Maple都有实现一阶导数、二阶导数、定积分和不定积分等微积分学中基本运算的函数。它还提供了多种有关三角函数运算的工具函数，包括高职阶段的诱导公式、倍角公式、降幂公式、和差化积公式、积化和差公式等多组三角函数公式，对高职的三角函数化简、证明、求值等提供了很好的支持。

除此之外，Maple提供了简单好用的GUI（图形用户界面）组件，如按钮、复选框、列表框、绘图框和滑动条等等。教师可以把运算命令行封装在这些组件中，制作成图形化的应用程序。在习题课上用它来制作某种题型的解题模板，将问题代入模板中进行验算，既能让学生清楚的看到解题过程，又能节省时间。例如求函数的极值的解题过程为：求导，解方程.f'（x）=0，观察图象，用驻点分割区间，分析单调区间，求极值。制作求函数极值的解题模板如图5-14所示，输入函数式即可分步得出解题过程，简单直观，一目了然。

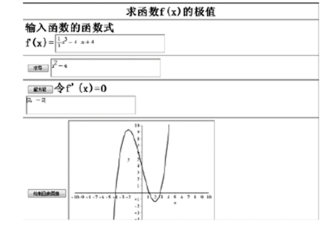
图5-14　求函数的极值的解题过程图

总结以上两点，绘制科学计算器与Maple的运算功能对比如表5-4所示。

表5-4　运算功能对比表

综上所述，Maple的运算功能要比科学计算器优越得多。Maple无误差的符号计算和高精度的数值计算能力，将复杂的问题交给计算机完成，能避免繁琐的求解过程，大大压缩课堂时间，节省老师工作，将更多的精力放在数学方法和数学思想的掌握上来。它强大的GUI（图形用户界面）更是方便教师验算，又为学生自学提供了方便。

（四）程序设计功能

算法思想是高职数学教学中的一条主线，已经成为了高职生不可或缺的数学素养。算法不仅是高职阶段的一门必修课，还是一种必须掌握的思想方法，贯穿于整个高职数学教学过程中解决多种问题。高职算法课程教学要求学生了解算法的含义、程序框图，掌握基本算法语句的使用。Maple为这部分内容提供了独立完善的编程系统，可以完整地支持高职算法教学的实现。

Maple程序命令类似C语言，简单易学，使用灵活多变，支持不同风格编写代码。综上所述，整个高职数学教学过程中，如果使用Maple为学生建立一个好的算法实现的程序语言平台。在这一平台上，教师鼓励学生编写程序来实现或验证算法思想，让抽象的算法思想变成生动形象的程序语言，通过程序语言的运行和调试来进行“数学实验”，许多传统方式不能解决的问题或不能讲清的数学概念都可以通过Maple的程序设计功能进行探究。教师引导学生观察和分析实验结果，以此来揭示抽象数学知识的产生和形成过程，发现数学问题的规律和本质，进一步培养学生利用信息技术获取知识和主动探究知识的能力，体验数学思想方法的真谛，体现学生的主体地位。