（一）运用Mathematica的现实条件

在传统的数学课堂教学中，教师是知识的传授者，是课堂的管理者。从建构主义的角度来看，教师的角色应该是学生学习的引导者和推动者。学生也不再是知识的被动接受者，而是应该成为知识的探索者和研究者。同时，课堂教学的主要形式不再是课堂讲解和布置作业，而是在教师指导下建构学生知识意义的过程。在技术应用方面，由于信息技术的广泛应用，教学内容展示不再是简单的粉笔黑板或PPT，而是基于信息环境的共享互动，集自主学习、交流反思、协作讨论于一体。

当前，高职学生的数学基础普遍薄弱，数学学习兴趣和自我效能感低下，很多时候其认知结构无法同化新知识，新的平衡无法建立，需要提供更多的帮助。

设想将课堂教学平台、实验教学平台和拓展教学平台等进行融合，并辅以相关资源，借助数学课程网站整合成数学课程资源平台。

整合后的课程资源平台可以更好地进行师生互动，便于师生同学间不受时空限制而进行交流。教师上课的录像、课堂笔记的扫描件、课件、辅导资料、课外阅读材料、常用数学软件等要满足学生的个性化需求，答疑、学法指导、作业、进度、满意度测评与成绩管理等模块让师生及时了解教学活动状态。还可将某些板块与学生邮箱关联，有内容更新时及时发通知到学生邮箱。

（二）Mathematica的特点

Mathematica软件包是一款集文本编辑、数值计算、符号运算、逻辑分析、图形、声音、动画和程序设计于一体的高度优化的专业系统，具有如下特点：内容丰富，功能齐全。初等数学、高职数学以及工程数学的各种数值计算和符号运算均可实现，画图功能强大。语法简捷，语句精炼。语法规则和表示更接近数学运算的思维和表达方式，用较少的语句即可完成复杂的运算和公式推导。操作简单，使用方便，命令易学易记，用户既可与之进行交互式对话，让它逐个执行命令，也可以让它对多个命令进行批处理。

目前，我国高等教育处于大众化阶段，2015年高等教育毛入学率已达40%。高校扩招造成大量中学文化基础薄弱的学生进入高职院校，这些学生数学基础参差不齐，而数学属于“强度框架”课程，按最近发展区理论教学实践中需要为他们搭建“脚手架”，否则难以达成课程目标。Mathematica可以实现初等数学、高职数学的各种数值计算和符号运算，画图功能强大，且语法规则接近数学运算的思维和表达方式，将Mathematica软件包融入高职数学教学中是可行的，这相当于为高职数学教师找了一个“助手”，为高职学生找了一个“帮手”。

以下用几个例子说明课堂上使用Mathematica软件辅助教学为何能提高教学效率。

例1：如何区分和理解极限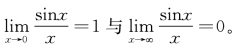

理论证明，学生往往很困惑而且在应用时经常发生混淆。课堂上教师利用Mathematica的绘图功能画出函数图像，可以使学生很清楚地区分这两个极限。

输入Plot［Sin［x］/x，｛x，-6，6｝］，Mathematica输出，如图5-1所示。

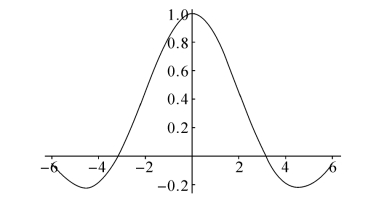
图5-1　自变量趋于0时函数变化趋势

输入Plot［Sin［x］/x，｛x，-100，100｝］，Mathematica输出，如图5-2所示。

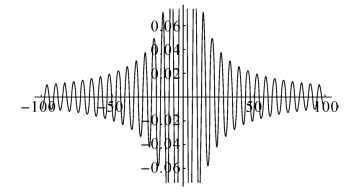
图5-2　自变量趋于无穷时函数变化趋势

从图5-1和图5-2可以看出这个函数当自变量x趋于0与趋于无穷时性态完全不同。这其中的第2个极限过程，如果不是借助函数图像是很难想象的。

例2：验证函数f（x）=4x3-5x2+x-2在区间［［0，1］上满足罗尔定理。

用作图命令画出f（x）的图像，输入f［x_］：=4x^3-5x^2+x-2，Plot［f［x］，｛x，-1，2｝］，则Mathematica输出图4-3。(www.daowen.com)

从图5-3可明显看出，f（x）在闭区间［0，1］上连续，曲线在开区间（0，1）上是光滑的，也就是说f（x）可导。

输入f［0］，f［1］，Mathematica输出f（0）=-2，f（1）=-2。从图上看，f（x）在x=0和x=1处的函数值的确相等，从而f（x）满足罗尔定理的第3个条件。

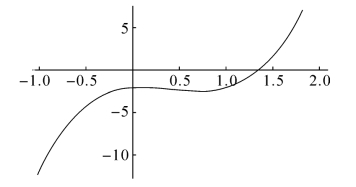
图5-3　验证罗尔定理的函数图像

输入f'［x］=D［f［x］，x］，Mathematica输出f'（x）=12x2-10x+1；输入Solve［f'［x］==0，x］//N，Mathematica输出f（x）的导函数在区间（0，1）内的两个零点：x1=0.116204，x2=0.717129。从图上看，曲线f（x）在这两个点的切线是平行于x轴的，即f（x）的导函数在这两个点的函数值为0。

从上述问题的求解过程看，基本上可以说每一步都消解了抽象、实现了“可视化”。

例3：从某工厂的某种型号的滚轴中任取20个，测得其直径数据如下（单位：毫米）。

13.26、13.63、13.13、13.47、13.40、13.56、13.35、13.56、13.38、13.20、13.65、13.69、13.42、13.29、13.51、13.46、13.48、13.53、13.58、13.48。

求样本均值、样本方差和标准差。

输入data=｛13.26，13.63，13.13，13.47，13.40，13.56，13.35，13.56，13.38，13.20，13.65，13.69，13.42，13.29，13.51，13.46，13.48，13.53，13.58，13.48｝；

Mean［data］

Variance［data］

StandardDeviation［data］

输出13.4515　0.0225397　0.150132。

（说明：在输入原始数据后，输入命令：Mean［data］，Mathematica输出样本均值x=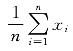；输入：Variance［data］，则输出样本方差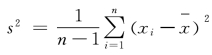；输入VarianceDeviation［data］，则输出样本的标准差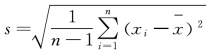，而且即使用户不会写“均值”“方差”“标准差”的英文单词，只要知道这个单词的前两个字母，比如“均值”的英文前两个字母是Me，当录入单词Me后，Mathematica系统会主动出示Message，Mean，Median，Medium，……等单词供用户选择，如果记住了单词的前三个字母，则系统主动出示的可供选择的单词就更好选择了，这极大了方便了高职学生，因为高职学生不只是数学基础薄弱，英语词汇也相对不足。）

例4：求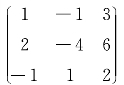矩阵的逆矩阵。

若按逆矩阵定义来求，学生兴趣索然，因为除了需要计算矩阵A对应的行列式的值，还要计算矩阵A的9个代数余子式的值，耗时而且容易出错，学生没有成就感，而借助Mathematica只需输入两个命令即可求出逆矩阵。

输入MatrixForm［A=｛｛1，-1，3｝，｛2，-4，6｝，｛-1，1，2｝｝］，Inverse［A］//MatrixForm；则输出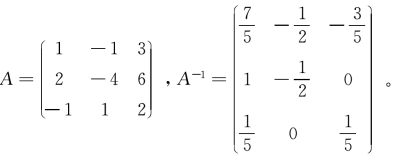

Mathematica处理冗长的计算迅速快捷，只需几个命令即可给出，对比较复杂的函数图像往往由一两个命令即可画出，通过直观显示而使教学内容生动形象，对提升学生学习兴趣有很大的促进作用。笔者认为，高职数学教学中融入数学软件对教学确实有很大帮助，而且会操作数学软件解决社会生活和工程设计中的实际问题是当代高职学生的一种必备素质。