数学实验是高职数学的一种最基本的数学学习活动，能使学生真切地体验如何“学数学、用数学”，感悟数学的形成过程，增强数学学习信念。在高职数学教学中开设实验教学，能加快高职学生数学学习观念的转变，坚持从学生的角度出发，在数学实验中增加课堂教学所缺失的实践环节，通过学生自己动手、动脑，让他们积极融入到数学学习过程中来。这样一来，对学生而言，除了能逐步培养学习数学的积极性、主动性，还能充分发挥个人的创造性、加强团结协作精神；从教师的角度来看，这种数学实验教学模式也是对传统教学方式的有益补充。同时在数学实验教学中引进先进的计算机技术工具，能进一步体现数学学科的实用性和现实性，借助观察、模仿、操作、猜想，形成对数学知识和问题进行分析、发现、应用明确的一种学习过程，在很大程度上带来高职在校生数学学习方式的改变，甚至革新，确定实践——认识——再实践——再认识的认识过程。学生在教师指导下，根据教师布置的实验内容，以一个研究者的身份参与到数学学习活动中来，将传统的“听数学”转变为当下的“做数学”，由过去的被动接受转化为现在的主动参与，能进一步填补学生对所学内容的体验环节，使学生在实践中消化，在消化中理解，在理解中掌握，实现良性循环，更利于对数学知识的理解与掌握，促进数学应用能力的提升。

当然数学实验教学改变了传统的数学理论知识传授，有助于激发学生的学习兴趣，增加了彼此在实验过程中的交流互动，调动了对解决数学问题的执著追求，出现了在图书馆查资料、向老师请教等多种学习方式，让高职学生的数学实验学习积极性空前高涨，大大体现了学生的主体地位。

数学实验是数学知识应用的一种形式，主要通过降低数学理论知识难度，化抽象为具体的方式帮助学生解决一些复杂的计算，从而节约时间，提高数学学习效率。在数学实验教学中“问题”是核心，为了更好地从问题出发进行探索与研究，就需要遵循一定的原则选择恰当的实验课题，具体包括：数学实验与理论相结合、学生为主体、典型性和趣味性相结合、直观性与抽象性相结合、个体研究与合作交流相结合、开发性与创新性相结合等原则。下面将按照数学实验教学模式，如图1-1所示，对函数实验案例进行研究。

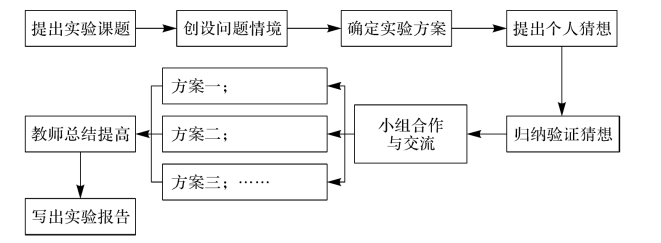
图1-1　高职数学实验教学模式

案例：函数y=Asin（ωx+φ）（x ∈ R，A＞0，ω＞0）的图像

（一）实验目标

（1）探索参数A、φ、ω对函数y=Asin（ωx+φ）图像的影响。理清函数y=Asin（ωx+φ）与函数y=sinx的关系，掌握函数y=Asin（ωx+φ）的作图方法。

（2）在经历了几何画板形象的演示之后，体验参数对函数的影响。让学生体验数学发现和创造的历程，培养学生探索数学现象的基本技能和基本能力。

（3）让学生自己操作，亲身体验，享受“做数学”的喜悦，培养他们的创新能力和合作精神。

（二）实验类型

探究性数学实验教学。

（三）实验工具

几何画板。

（四）实验过程与分析

（1）参数A的变化对函数y=Asin（ωx+φ）图像的影响。利用几何画板在同一个坐标系中做出函数y=sinx，y=sinx的图像，对各函数图像进行观察和比较，思考参数A的变化对函数图像的影响。

观察每一组图像的性质区间及其图像间相互关系、特点，分组讨论、交流。

学生观察图像，填写下表1-1。

表1-1　函数实验记录表

学生讨论交流，归纳总结，提出猜想：每组函数图像之间都有一定的伸缩关系。然后利用几何画板动态的演示来说明其猜想的正确性，如图1-2所示。

图1-2　函数几何画板动态演示（1）

拖动点D，观察图像上B、C的运动，在横坐标相同的条件下，纵坐标的变化，同时注意比值的变化。

继续利用几何画板演示，改变A的值，整体对比函数y=sinx与y=Asinx的关系，进一步引导学生观察、讨论、交流，说出体会。再通过如图1-3的演示，进一步巩固学生的猜想。

(www.daowen.com)

图1-3　函数几何画板动态演示（2）

教师总结：随着参数A的变化，函数图像只是在竖直方向被拉长或缩短了。在此基础上引导学生总结归纳图像变换的特点和规律。

（2）参数ω对函数y=Asin（ωx+φ）图像的影响。仿照参数A对函数y=Asin（ωx+φ）图像影响的实验步骤进行探索。

利用几何画板在同一个坐标系中做出函数y=sinx、、y=sin2x的图像，对各函数图像进行观察和比较，思考参数ω的变化对函数图像的影响。观察每一组图像的性质、特点，发现定义域、值域都一样，周期是多少看不出来，每组函数的周期显然是在变化的。这样可以引导学生得出结论：参数ω的变化会引起函数周期的变化。

学生继续观察，分组小组讨论、交流。通过以下演示归纳、总结出参数ω是如何影响周期变化的，如图1-4所示。

图1-4　函数几何画板动态演示（3）

首先拖动点D（点B、C分别在它们各自的图像上），在纵坐标相同的情况下，观察点B、C横坐标的变化，以及比值的变化。

然后改变ω的值，进一步观察函数y=sinx与y=sin（ωx）的图像关系。教师引导，鼓励学生用自己的语言描述演示过程中的现象，最后教师在学生归纳的基础上给出参数ω的变化对函数图像的影响：随着参数ω的改变，函数图像只是在水平方向被拉长或缩短了，即由函数y=sinx变换到函数y=sin（ωx）的过程中，在不改变图像上点的纵坐标的情况下横坐标伸长（0＜ω＜1）或缩短（ω＞1）为原来的倍。这种变换成为周期变换。

（3）参数φ对函数y=Asin（ωx+φ）图像的影响。仿照参数A对函数y=Asin（ωx+φ）图像影响的实验步骤进行探索。

利用几何画板在同一个坐标系中做出函数y=sinx，y=，y=的图像，对各函数图像进行观察和比较，思考参数φ的变化对函数图像的影响。

观察每一组图像的性质特点，发现定义域、值域、周期都一样，只是函数图像的位置发生移动。学生提出猜想：参数φ的变化会引起函数图像的左右平移。教师继续下面的演示，学生观察当φ取不同值时，图像是如何平移的，如图1-5、1-6所示。

当φ＞0时

当φ＜0时

图1-6　函数几何画板动态演示（5）

图1-5　函数几何画板动态演示（4）

学生通过观察可得出结论：随着参数φ的改变，函数在水平方向的位置发生了变化，由函数y=sinx变换到函数y=sin（x+φ）的过程中，图像上所有的点向左（φ＞0）或向右（φ＜0）平移了|φ|个单位。这种变换称为平移变换。

（4）参数A，φ，ω对函数y=Asin（ωx+φ）图像的影响。以为例，探究如何由函数y=sin x经过图像变换得到函数y=Asin（ωx+φ）的图像。

学生根据上面的探索小组讨论、交流图像变换的方式。

（五）实验效果评价

三角函数图像变换教学是个难点，需要反复对函数图像进行操作来讨论函数图像之间的变换关系，因此，利用计算机软件作图进行教学会比较轻松。这节课通过设置探究性实验追踪图像上的点及图像的变换，来演示函数y=Asin（ωx+φ）图像的产生、变换过程，揭示参数对函数图像的影响，学生可以直观、清晰地观察图像的变换过程，更容易加深对图像变化和生成的理解。在课堂上，教师指导学生操作实验，观察绘图过程中的图形变换，发现规律，验证结论，填写实验报告，获得数学真实。在这个过程中，学生可以体验到数学发现和创造的魅力，这不仅有利于学生思维能力和实践能力的培养，也有利于学生创新意识和探索能力的培养。

当然提高高职数学课堂教学有效性策略除了教学实验的开展以外，还可以从有效准备、有效课堂讲授、有效课堂提问、有效激励、有效习题设计、有效教学反思等方面入手，共同为高职数学课堂教学的有效性的提供服务。