一元波动方程式的分解

波动方程式的分解

●沿z轴正方向传播的平面波

电场沿x方向的偏振波

电场与磁场

●平面电磁波的瞬时分布

平面电磁波

注：理解关于电场和磁场的最简单的波动方程。

[1]一元波动方程

一元波动方程为

φ（x，t）为空间中（一元）的任意

时间函数

c为传播速度（m/s）

一元波动方程的分解

φ（x，t）=f+（x-ct）+f-（x+ct）

f+（x-ct）为行波

f-（x-ct）为反射波

[2]平面电磁波

沿z轴正方向传播的平面波为

相应地

E_x、E_y为x、y方向的电场强度分量（V/m）

H_x、H_y为x、y方向的磁场强度分量

H_x=B_x/μ、H_y=B_y/μ（A/m）

ε为空间介质的介电常数（F/m）

μ为空间介质的磁导率（H/m）

一元波动方程的分解

空间和时间的任意函数，均可用来描述波动在空间中随着时间的变化而进行传播的过程。为简单起见，在一个方向上以速度c（m/s）传播的波函数φ，其一元波动方程为(www.daowen.com)

在t=0时刻的波形φ（x）=f+（x），以速度c（m/s）在x的正方向以移动。在时间为t（s）时刻的波形为

φ（x，t）=f₊（x-ct）

同理，在x轴负方向移动的波形为

φ（x，t）=f_-（x+ct）

将上述一元波动方程的分解式，通过叠加原理表示为

φ（x，t）=f+（x-ct）+f-（x+ct）

式中，右边第一项为行波，右边第二项为反射波。

平面电磁波

分别存在于x、y坐标平面上的电场强度为E的电场和磁场强度为H（=μB）的磁场，沿z方向上传播形成的电磁波为平面电磁波。

在z方向上传播的平面波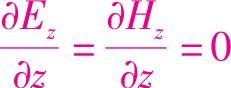，，，因此E_z=H_z=0，传播方向上的振动分量为0。

假设只有x方向的电场强度分量时，平面波的波动方程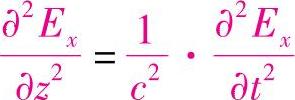为其分解式为

E_x=f+（z-ct）+f-（z+ct）

为简单起见，仅考虑在z的正方向上传播的分量，则有

E_x=f+（z-ct）

E_y=E_z=0

又因为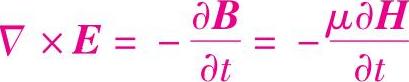，相应的磁场强度为

由此可见，当电场强度的x分量在z方向传播时，磁场强度的y分量也以与电场强度同波形和同相位在z方向传播。电场波和磁场波的振动方向均与其传播方向垂直，因此也将平面电磁波称为横向波。

同理，当电场分量位于y平面时，其相应的电场强度与磁场强度的分量为

例题1

如图所示，真空中的平面电磁波沿z轴的正方向传播。电场强度的x分量为E₀sin（kz-ωt），y和z分量为0。求磁场强度的y分量。

【例题1解】

平面电磁波电场强度为E_x=E₀sin（kz-ωt），E_x=E_z=0。磁场强度的x和z分量为0。由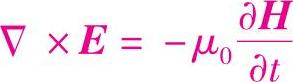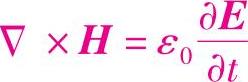，，得磁场强度的y分量为

上述两个等式中，c₁（t）=c₂（t）=0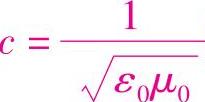，因此有

磁场强度H_y（A/m）的y分量为

与电场强度同相位。