【摘要】:[1]标量的梯度标量函数的梯度为gradf=ff为标量函数为矢量微分算子矢量微分算子为[2]矢量的散度矢量的散度为divA=·AA为矢量[3]拉普拉斯算子标量函数梯度的散度div=·=2f拉普拉斯算子为标量的梯度电场中的电位可以用电场强度的梯度来表。梯度的大小为矢量的散度电场强度的分布,可以采用矢量的散度算子来表示。矢量A的散度,可用矢量微分算子表示为拉普拉斯算子如果矢量A为标量函数f的梯度,则矢量A的散度为Δ2为拉普拉斯算子,又称调和算子。
标量函数的梯度:gradf
标量的梯度
●电场强度分布情况用矢量散度来表示
矢量A的散度:divA
矢量的散度
●标量函数梯度的散度
拉普拉斯算子
注:学习矢量分析的基础。
[1]标量的梯度
标量函数的梯度为
gradf(x,y,z)=∇f
f(x,y,z)为标量函数
∇为矢量微分算子
矢量微分算子为
[2]矢量的散度
矢量的散度为
divA=∇·A
A为矢量
[3]拉普拉斯算子
标量函数梯度的散度
div(gradf(x,y,z))=∇·(∇f)=∇2f(https://www.daowen.com)
拉普拉斯算子为
标量的梯度
电场中的电位可以用电场强度的梯度来表。标量函数f(x,y,z)的梯度可用矢量微分算子∇表示为
∇为矢量微分算子。梯度的大小为
矢量的散度
电场强度的分布,可以采用矢量的散度算子来表示。矢量A的散度,可用矢量微分算子∇表示为
拉普拉斯算子
如果矢量A为标量函数f(x,y,z)的梯度,则矢量A的散度为
Δ2为拉普拉斯算子,又称调和算子。
算子∇的相关公式
φ,ψ,u,v是x,y,z的函数,位置矢量r为
r=ix+jy+kz
r0是r方向的单位矢量,则各函数的梯度如下:
例题1
如图所示,点P的电位为V=Q/4πε0r,求电场强度矢量。这里,位置矢量r为r=rr0=ix+jy+kz,r=(x2+y2+z2)1/2。
【例题1解】
电场强度矢量为E=-ΔV。
因为r=(x2+y2+z2)1/2,所以其x方向的分量为
同理,其y,z方向的分量为
因此有,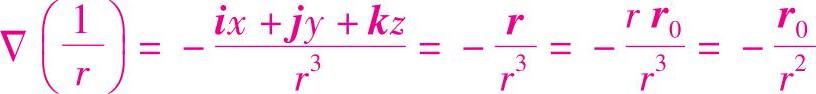
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。
相关文章







