导体中流过电流的情况

导体流过的电流产生磁场的方向

●导体中微小单元流过电流产生磁场的大小

毕奥-萨伐尔定律

●环形回路电流在其轴线上产生的磁场

环形回路电流产生的磁场

注：当磁场用矢量来表示时，电流产生的磁场为电流矢量的外积。

[1]毕奥-萨伐尔定律

微小导体流过电流时周围P点的磁通密度dB（T）为

I为导体中流过的电流（A）

dl为导体的微小单元长度（m）

r为dl附近P点到导体线的距离（m）

r₀为距离r的单位位置矢量

标量表示形式：

θ为dl的电流的方向与P点的方向的夹角（rad）

[2]环形回路电流中心轴上的磁场强度

环形回路的导体中流过电流时，在中心轴的P点处产生的磁通密度B（T）为

I为导体中流过的电流（A）

a为环形回路的半径（m）

z为环形回路的圆心与P点的距离（m）

环形回路的圆心流出的磁通密度B（T）为(www.daowen.com)

毕奥-萨伐尔定律

在导体中流过的电流为I（A）时，根据安培右螺旋定则可知，电流所产生的磁场在P点处的方向是垂直于导体并向着纸面的方向的。因此，在导体上任意一O点处，微小长度为dl（m）的导体单元中流过的电流为I（A）时，在与O点的距离为r（m）的P点处，所产生的磁场的磁通密度dB（T），与电流I（A）、微小长度dl（m）以及电流的方向与OP之间的夹角θ（rad）的正弦成正比，与OP的长度r（m）的平方正反比，这种关系，称为毕奥-萨伐尔定律。

环形回路电流中心轴上的磁场

环形回路导体的微小单元dl中流过的电流，在中心轴上的P点处产生磁场的磁通密度dB。此时dl的电流方向与P点的位置矢量是垂直的，根据毕奥-萨伐尔定律的表达式可得夹角θ=π/2。因此，P点处的磁通密度dB（T）为

这里，dl的方向与位置矢量r的方向垂直。该磁通密度在环形回路中心轴方向上的分量dB_z（T）为

dB_z=dBsinα

式中，sinα=a/r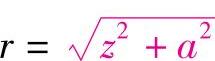，代入得

因此，整个环形回路电流所产生的磁场的磁通密度在中心轴上的分量B_z（T）为

在与环形回路平行的平面上，所有电流单元dl产生的磁场的磁通密度平行分量，在沿着环形回路上的线积分时相互抵消。因此，整个环形回路电流产生的磁场的磁通密度B（T）即为其在中心轴上的分量B_z（T）。亦即

B=B_z

当z=0时，环形回路的中心的磁通密度B（T）为

例题1

如图所示，真空中放置半径为a=10cm的环形导体，当导体中的电流I=20mA时，计算环形导体中心轴上、与导体中心距离为z=1m的P点处所产生磁场的磁通密度。

【例题1解】

在P点处所产生磁场的磁通密度B（T）为

例题2

在真空中，当半径为a（m）的环形导体中流过的电流为I（A）时，试求环形导体的中心O点处所产生的磁通密度。

【例题2解】

环形导体的微小单元dl流过的电流在中心O点处产生的磁通密度dB（T）为

整个环形电流在中心O点处产生的磁通密度B（T）为