空间点电荷的情况

等位面

●等位面与电力线的关系

等位面与电力线

●电位的梯度

电场中电位梯度与电场强度

注：电位梯度即是电场强度。使用通过第5课学习的全微分进行了解。

[1]电位梯度

空间中电位梯度，可以用全微分dV（V/m）来表示：

V（x，y，z）为电位（V）

[2]电位梯度与电场

电位梯度与电场强度的关系为

E为电场强度（V/m）

电场强度在x、y、z方向上的分量：

空间中的等位面上的点的电场强度

等位面

电场中的所有电位相等的点所构成的平面称为等位面。空间中有一点电荷，以点电荷为中心，以与点电荷距离r（m）为半径的球面，在该球面上的电位都相等。此时，以该电荷为中心的球面称为等位面。

对于等位面，有以下一些共同的性质：

①等位面与电力线都是垂直相交的；(www.daowen.com)

②不同的等位面之间是不可能相交的。

电位梯度

有空间的P点，如果其周围的电位分布已知，并以矢量的形式来表示，则该点的电场强度在x、y、z方向的分量，以及该点电位梯度在x、y、z方向的分量均可根据电位分布计算出来。

该点的电位V（x，y，z）的梯度可用全微分dV（V/m）表达：

将V=-∫_∞^PE·dl微分得

dV=-E·dl=（E_xi+E_yj+E_zk）·（dxi+dyj+dzk）

因此，电场强度在x、y、z方向的分量为

例题1

如图所示，真空中有半径为3cm的圆环，电荷量2×10^-8C均匀分布在圆环上。位于圆环中心轴上，距离圆环中心4cm。计算P点的电场强度。

【例题1解】

圆环上的微小长度dl的电荷量用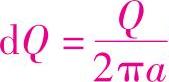来表示，这些电荷在P点产生的电位为

整个圆环在P点产生的电位V（V）为

P点在中心轴（x）方向的电场强度E_x（V/m）为

例题2

当空间中的电压分布为V=3x+2y-9z时，试计算其电场强度的分布。

【例题2解】

电场强度E（V/m）的分布为