有点电荷时：

电力线的形状

●以点电荷为中心半径为r的球面S表示为

电场强度的高斯定理

●带电导体球内外的电场

导体内外的电场强度

注：关于面积分参见第4课的内容。

[1]电力线

以点电荷为中心的任意球面，单位面积上的电力线的条数：

Q为电荷量（C）

N为电力线的总数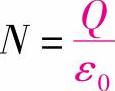，（条）

r为球面的半径（m）

S为球的表面积，S=4πr²（m²）

E为电场强度（V/m）

[2]电场中的高斯定理

电场中的高斯定理为

E为电场强度（V/m）

n₀为闭合曲面S上的任意一点的法线方向的单位相量

Q_i为闭合曲面上的电荷量积分表达式为

E_n为电场强度的面法线方向的分量（V/m）

E为电场强度（V/m）(www.daowen.com)

θ为E与n₀夹角

任意闭合曲面内，当有多个点电荷存在时，相当于单个电荷情况的叠加。

电通

电力线的方向以及密度表示了电场强度的方向和大小，从点电荷Q（C）共发射出Q/ε₀个电力线，空间中任意一点的电力线的密度，表示为该点的电场，电力线分布的密度通常用电通来表示，电通是从点电荷Q（C）闭合曲面穿过的电力线的总数Q条。

电场中的高斯定理

在空间中放置一点电荷Q（C），电力线由电荷呈放射状传播，以点电荷为中心做一半径为r（m）的球面，则所有电力线均垂直穿过该球面，其总数为

穿过球面的电力线个数与球面的半径无关，球面上穿过的电力线的总个数等于Q/ε₀（个）。这个结论不仅适合于该特殊的球面上，对于任意闭合曲面也同样成立，这就是高斯定理。

一般，在电场中的任意闭合曲面上，穿过曲面的所有电力线的总个数为，闭合曲面电场强度的法线分量E_n的面积分：

如果，闭合曲面内有n个点电荷Q_i（i=1，2，…，n）同时存在的情况下，则穿过闭合曲面的电力线的总数为

例题1

如图所示，包含有点电荷2×10^-6C、-4×10^-6C、8×10^-6C的闭合曲面上，垂直发出的电力线的总个数是多少？

【例题1解】

电力线的总个数为

例题2

电荷Q（C）的带电导体半径为a（m）的球体。求导体内外的电场强度。

【例题2解】

将导体以及导体以外的任意空间看作是半径为r的虚拟闭合球面S，从闭合曲面垂直穿过的电力线的强度，也就是电场强度，在闭合曲面上的任何一点都是相同的，根据高斯定理，下式成立：

在导体球以外的空间（r≥a），其电场强度E（V/m）为

在导体球的内部（r<a），由于导体的电荷都集中分布在导体的外表面，内部电荷Q=0，所以其内部电场强度E（V/m）为

E=0