两个点电荷Q（C）之间的作用力F（N）：静电力

静电力（库伦力）

●多个点电荷之间的作用力：

叠加原理

●任意3个点上的电荷作用力

库伦力的合成

注：静电力为矢量，关于力的合成知识复习第2课。

[1]库伦定律

两个点电荷之间的作用力F（N）为：

Q₁Q₂为电荷（C）

r为电荷间的距离（m）

k为真空中的比例系数（空气中的也几乎相同），

力的方向：在两个电荷所确定的直线上，当两电荷的符号不同时为引力，符号相同时为排斥力。

[2]库伦定律的矢量表示

库伦定律的矢量表达式为

r₀为电荷之间作用力的单位矢量

r为电荷之间的距离

两个电荷Q（C）之间的作用力F（N），通常把相互之间的排斥力作为正方向

库伦定律

真空中或空气中的两个带电体，当带电体之间的距离比带电体的大小充分大的时候，相互之间的作用力可以看作与点电荷之间的作用力类似。两个带电体之间作用力的大小与两个带电体的电荷的乘积成正比，与两个带电体之间的距离的二次方成反比，该静电力也称为库伦力。

力的方向在带电体连线的方向上，相互作用力方向向外的，称为排斥力，记为正。(www.daowen.com)

多个点电荷之间的作用力

电荷之间的作用力，大小和方向都可以用矢量来表示，多个点电荷存在的情况下，求其中的某个电荷上（里）的作用力，需要考虑除此电荷之外的其他各个电荷与该电荷之间的相互作用力，然后用矢量合成来表示该矢量的大小和方向。

在多个点电荷同时存在时，任意两个电荷之间独立的作用力，不会因为其他电荷的存在而改变。因此，可以通过分别计算两两电荷之间的作用力，然后通过矢量合成而计算最终的合力，也就是实际的作用力，这种方法称为叠加原理。

例题1

如图所示，真空中的两个电荷电量分别为3×10^-6C、1.2×10^-5C，它们之间的距离为9cm，求两个电荷之间的静电力。

【例题1解】

两个电荷之间的静电力F（N）为

例题2

如图所示，一个边长为6cm的等边三角形，以为顶点，2×10^-6C、-2×10^-6C、2×10^-6C的三个点电荷分别位于三角形的三个顶点ABC的位置，求顶点A所受到的静电力。

【例题2解】

顶点AB间的静电力为

顶点AC间的静电力为

如图所示，顶点A所受的静电力F_AB和F_AC的合力大小为

F_A=|F_AB|=|F_AC|=10N

例题3

在例题1的条件下，A、B两点所定的一条直线上，放置另一个电荷于A、B点之间，求在A、B点之间的电荷所受合力为0的位置。

【例题3解】

假设电荷Q位于A、B点之间的C点的位置，当A、C点之间的距离为x时，在C点上的电荷受到的力F_CA、F_CB（N）为

因为，这两个力是正反作用力，F_CA=F_CB，所以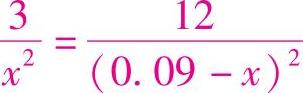：，x=0.03m或=-0.09m

到A点的距离为3cm时，它所受到的静电力的合力为0。