空间（xyz坐标系）作曲面

多元函数

●若多元函数f（x，y，z）在定义域内是连续的，则其偏导数：

y、z可看作常数：

偏导数的定义

●多元函数f（x，y，z）的梯度：

全微分的定义

注：偏微分与全微分通常用于求取电物理量在已知空间中的分布斜率（变化率）。

[1]偏导数定理

可连续微分的多元函数f（x，y）中，存在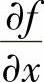、、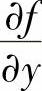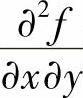时，则

[2]复合函数的偏导数

如果f（x）、g（x）都是可连续微分的函数，h（f（x）、g（x））是关于f、g的可以连续偏微分的话，则有

如果f（x，y）、g（x，y）都是可连续微分的函数，h（f（x，y）、g（x，y））是关于f、g的可以连续偏微分的话，则有

偏导数

函数f（x，y，z）是连续的三元函数。如果把y、z看作常数的话，把函数f（x，y，z）成为只是x的函数。把f（x，y，z）只对x求导数称之为f（x，y，z）对x的偏导数。同样地，可对y、z求导数就为x、y、z的偏导数，又称为偏微分。

全微分

多元函数f（x，y，z）的梯度全微分求用得，可用以下多元函数f（x，y，z）的泰勒展开式为(www.daowen.com)

式中，Δx、Δy、Δz表示非常小的变化量，忽略二次项以后各项，则有

Δf=f（x+Δx，y+Δy，z+Δz）-f（x，y，z）

当Δx➝0，Δy➝0，Δz➝0时该式的极限，就是全微分表达式：

希腊字母表

希腊字母（Greek Alphabet）经常被作为符号使用。

例题1

试求f（x，y，z）=2x²yz³-3xy³函数的偏导数。

【例题1解】

关于x的偏导数

关于y的偏导数

关于z的偏导数

例题2

试求f（x，y，z）=2x²yz³-3xy³函数的全微分。

【例题2解】

f（x，y，z）=2x²yz³-3xy³的全微分：