1.着手非线性分析

花一些时间来认真研究并进行分析，可以避免很多与非线性分析有关的困难。下面的建议对读者应当有所帮助。

如果用户在以前未应用过某一种非线性特性，则应当在分析大型、复杂的模型之前，首先建立一个简单的模型（即只包含几个单元的模型），并确保对其特性有所了解。

保持最终模型尽可能简单。如果可用二维平面应力、平面应变或轴对称模型来代表三维结构，那就这么做。如果可通过对称或反对称面来使模型规模减小，那就这么做。然而，如果荷载是反对称的，则通常不采用反对称的特点。反对称也可能在大变形分析时不适用。如果忽略某一非线性细节而不会影响模型关键区域的结果，那么就应该这么做。在可能时，用静力等效荷载来模拟瞬态动力荷载。

应当认识到，在经受塑性变形的区域，要求相当的积分点密度。低阶单元提供了与高阶单元相同的积分点数目，因此在塑性分析中应用低阶单元较为合算。在塑性铰区域，网格密度尤其重要。在接触表面要有足够的网格密度，以使接触应力分布较光滑。

为了求解应力，也要有足够的网格密度。需要计算应力或应变的区域要比位移或非线性解析区域网格要密一些。需要高阶模态时，网格密度要足够。需要的单元数目，取决于单元假定的位移形状函数，以及模态形状本身。对于瞬态动力波传播，要采用足够密的网格。如果波传播很重要，则一个波长最小要20单元。(www.daowen.com)

对于非保守、路径相关系统，施加荷载时要用足够小的荷载增量，以保证分析接近荷载-响应曲线。有时，可以逐渐地加载，而使保守系统的收敛行为有所改进，这样可使Newton-Raphson平衡迭代数最小。

2.克服收敛问题

收敛失败可能表示结构产生物理上的不稳定性，也可能仅仅是由有限元模型中的某些数值问题引起的。在执行非线性分析过程中，ANSYS在每个迭代期间根据收敛准则计算收敛模。批命令方式和交互方式均可应用的图形求解追踪（GST）特性，在计算过程中将显示计算的收敛模以及准则。典型的GST显示如图11-3所示。

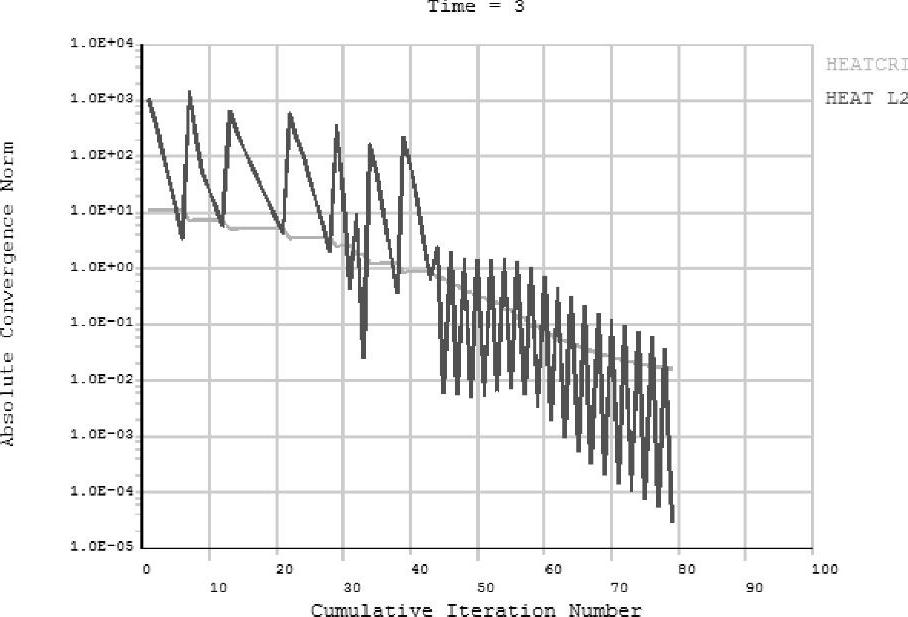
图11-3 有GST特性显示的收敛范数