上节中我们得到一个数字2.7183…，它是一个无理数，在高等数学中起着至关重要的作用，一般用e来标记，并用下面的级数来求它的近似值：

在上节关于存款按复利方式增长的例子中，我们得知e就是式子

在n趋于无限大时的极限值。

鉴于很多无法详述的原因，我们把e作为自然对数的底非常方便。

自然对数表很久以前就有，并在科学技术中起到非常重要的作用。我们在前面讲到了48位、61位、102位，甚至260位的对数“巨人”，都是将e作为底的对数。

此外，数e还总是在意想不到的地方出现，比如这个问题：如果想把数a分为若干份，怎样分才能使每一份的乘积最大？

前面已经讲过，如果和为定值的一组数，当这组数中的每个数都相等时，它们的乘积为最大值。因此，这里的a需要平均分，应该怎样分呢？由高等数学的知识得知：当分成的每一份同e最接近时，乘积可以得到最大值。

例如，设a等于10，应该如何平均分？我们可以先求出e除a的商，得(www.daowen.com)

由于一个数不可能被分成3.678…份，所以取最接近此数的整数，即4。因此，分成的每一份为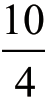，也就是2.5时，各项乘积最大，这4份的乘积为

2.54=39.0625

可以验证此结论是否正确，如果把10平均分成3份或5份，得出的乘积分别为

显然，它们的结果都比前面小。

如果a等于20呢？那么就得平均分为7份，原因是

如果a等于50，就分为18份；如果a等于100，就分成37份。原因是

数e不仅在数学领域，在物理学、天文学和其他领域中都发挥着至关重要的作用。比如在下面的问题中，经常会用到数e：计算火箭速度的奧尔科夫斯基公式，放射性元素的衰变，气压随高度不同而发生变化的公式，欧拉公式，细胞的增殖问题，摆锤在空气中的摆动，物体的冷却规律，地球年龄，线圈中的电磁振荡等等。