前文牛吃草问题是根据牛顿的牛吃草问题变化而来。下面，我们就来看看牛顿的那个题目。

有3个牧场，面积分别是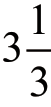公顷，10公顷和24公顷。3个牧场上草的长速、密度相同。在第一个牧场饲养12头牛，草可供牛吃4周；在第二个牧场饲养21头牛，草可供牛吃9周。那么，要想第三个牧场的草供牛恰好吃18周，应该饲养多少头牛？

【解答】这里我们同样需要借用辅助未知数y，用来表示1周内每公顷牧场上新长出的草占原来牧草总量的比重。先来看第一个牧场，1周后，新长出的草是原有草总量的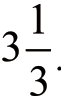y倍，新长出的草就是原有草总量的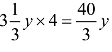倍。

相当于第一个牧场面积变大为公顷。

即牛在4周内吃草面积为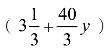公顷。

那么，12头牛在1周内吃草的数量为上数的，而1头牛在1周内吃掉的草就是上数的，即

也就是说，1头牛在1周内一共吃了面积为公顷的草。

同样，我们可以计算出第二个牧场1头牛一周内能吃掉牧场上多大面积的草。

一周后，1公顷牧场上长出的草是y；9周后，1公顷牧场上长出的草是9y，而10公顷牧场上长出的草是90y。(www.daowen.com)

也就是说，21头牛在9周内吃掉相当于面积为（10+90y）公顷的草。

可得，1头牛1周内吃草面积是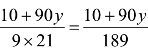公顷。

由于每头牛每星期的吃草量相同，所以

得出

据此，我们就能够计算出1头牛在1周内的吃草量：

到这一步，我们就很容易解出问题答案。设第三个牧场上共有牛数为x，那么

解出x=36。也就是说，如果想让第三个牧场的草恰好能吃18周，需要饲养36头牛。