传统的空间尺度上推和空间聚合方法多是在假设传感器的成像函数为一个标准矩形窗函数的理想状态的前提下，采用多像素平均的算法由多个高空间分辨率遥感像元聚合得到低空间分辨率的一个像元值，这也是本研究上述尺度误差分析的假设之一。虽然该方法可以相对准确地描述空间尺度变化的影响，但由于遥感传感器的成像函数并不是一个标准的矩形窗函数，因此该假设仍会带来地表参数估计的误差。尤其是对于水环境遥感定量产品来讲，往往自身的变化程度比较低，更需要精确地去除由于不精确的空间尺度转换引入的误差。

真实状况下的传感器成像过程并不是传感器视场内的像元辐射或者发射值的算术平均值，而是受到传感器电子和光学元件自身特征的影响，是中心视场单元和中心像元之间根据距离的相对权重加权值。描述传感器成像过程中不同位置加权值的函数叫做传感器的点扩散函数(Point Spread Function，PSF)。因此在进行遥感数据的空间尺度转换时，通过高空间分辨率的遥感数据与对应传感器的点扩散函数的空间加权，可以获得更接近真实值的低空间分辨率遥感数据。常用的传感器点扩散函数多以高斯函数模拟，如公式(5-9)所示。其中x，y为当前的中心像元位置，u，v是邻近像元与中心像元的坐标，σ是传感器的空间分辨率的1/2值。公式(5-10)和公式(5-11)给出了通过点扩散函数空间聚合到低空间分辨率的遥感反射率数据，然后利用悬浮泥沙反演模型获取悬浮颗粒物的过程。

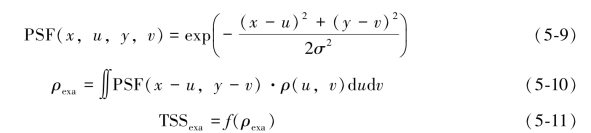
图5-16展示了基于点扩散函数PSF的高空间分辨率通过尺度转换为低空间遥感影像数据的示意图。图5-17为本研究采用的多空间尺度的点扩散函数PSF的模型，以16 m的GF-1 WFI高空间遥感数据为基础，分别实现了32，96，256，496，756和992 m的逐级降低的低空间分辨率遥感数据。

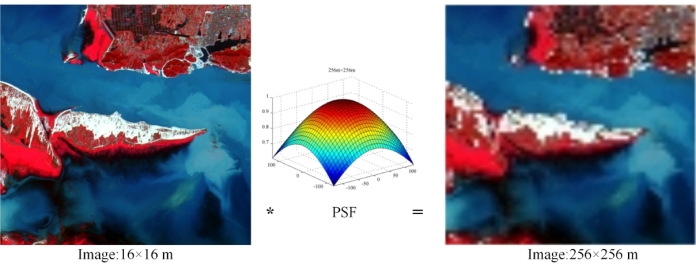
图5-16　基于理论点扩散函数(PSF)的尺度转换原理示意图

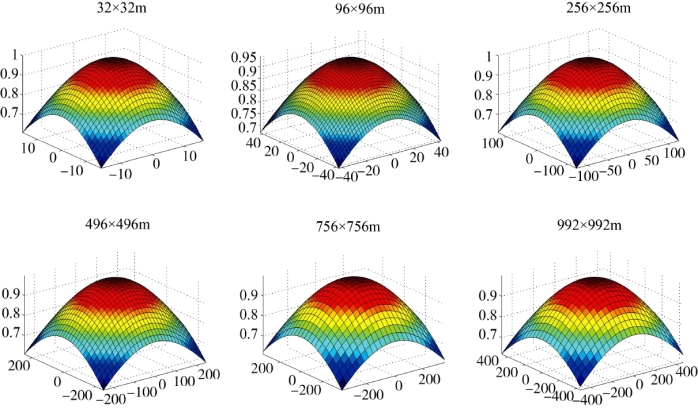
图5-17　本研究用到的多空间尺度转换的点扩散函数原型

以基于点扩散函数PSF的空间尺度转换方法为基础，对比分析了广泛使用的基于像元平均的空间尺度上推方法的精度和有效性。图5-18给出了两种转换方法的相关性和差异性分析结果的强度散点图，其中红色实线为1∶1对角线，分别针对32，96，256，496，756和992 m的6种空间尺度转换的结果进行了相关性分析。结果显示两种方法的相关性在各个尺度上都表现较高(R2＞0.99)，但是随着空间尺度的不断降低，两者线性回归的斜率逐渐增大。在32 m的空间尺度上，像元平均法相对于点扩散函数法的回归函数的斜率小于1，这意味着在当前尺度下，像元平均法所得到的遥感反射率数据呈现低于点扩散函数的数据的整体趋势。

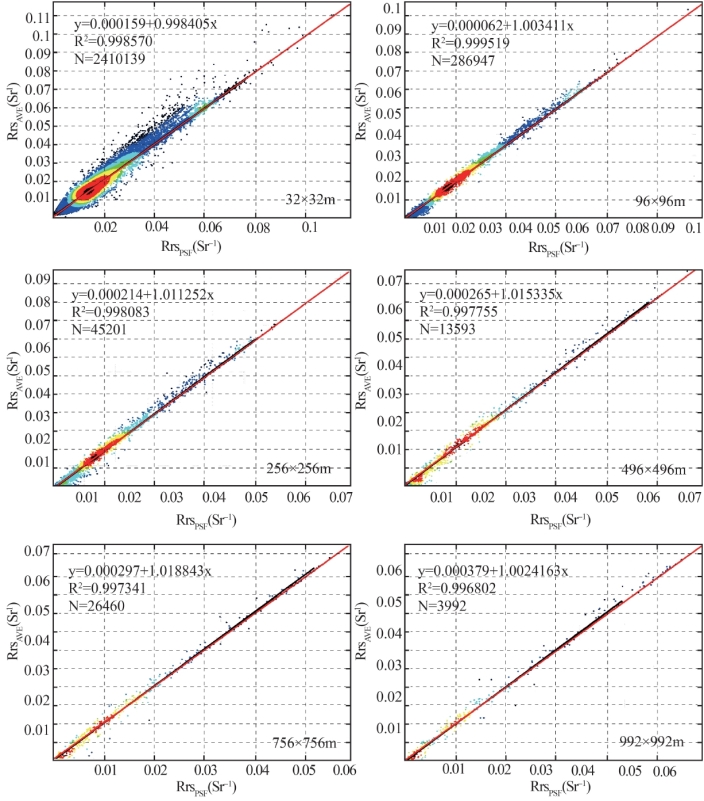
图5-18　基于点扩散函数和像元平均的空间尺度转换方法的水体遥感反射率数据对比分析图

然而随着空间尺度的降低，两者的回归斜率逐渐增大，在96 m空间尺度的时候，基于像元平均法得到的遥感反射率数据开始呈现出大于基于点扩散函数的趋势，并且该趋势随着尺度的降低而增大，其斜率分别为0.998，1.003，1.011，1.015，1.019，1.024。由于回归函数的截距非常小且接近于0，因此可以认为斜率直接反映了两者之间的大小关系。虽然两种方法得到的遥感反射率数据结果相关性较高，且相对偏差量级较小，然而由于水环境参数定量遥感反演使用较多的非线性模型，可能导致水环境参数产品误差的急剧增大。

为了分析不同空间尺度转换方法的水环境遥感产品的尺度误差，本研究利用16 m高空间分辨率数据，采用三种空间尺度转换方法分析了悬浮颗粒物产品的误差空间分布及趋势图。第一种转换方法是采用点扩散函数方法进行空间尺度转换，得到低空间分辨率的遥感反射率数据，然后通过上文得到的悬浮颗粒物反演模型，获得低空间尺度的悬浮颗粒物产品，并以此为基础评价其他两种转换方法的产品误差；第二种方法为采用空间像元平均方法得到低空间分辨率的遥感反射率数据，然后通过相同的悬浮颗粒物模型，得到低空间分辨率的悬浮颗粒物产品；第三种方法为在高空间分辨率遥感数据的基础上，直接采用悬浮颗粒物反演模型下获得悬浮颗粒物产品，然后利用空间像元平均的方法，计算得到低空间分辨率的悬浮颗粒物产品。

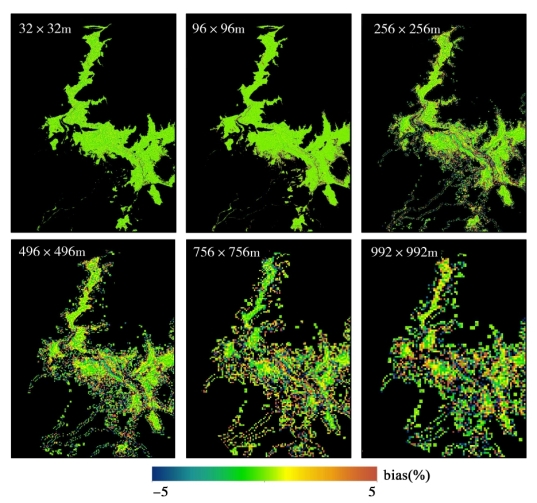
图5-19　基于遥感反射率数据像元平均法与点扩散函数法的鄱阳湖悬浮颗粒物反演误差趋势分布图

图5-19和图5-20分别给出了基于遥感反射率数据像元平均法与点扩散函数法和基于悬浮颗粒物产品像元平均法与点扩散函数法的鄱阳湖悬浮颗粒物反演误差趋势分布图。两个误差分析的结果都是以基于点扩散函数法的结果作为基准，结果显示两种空间转换方法的尺度误差都具有典型的随空间尺度增大而显著增大的整体趋势。如图5-22所示，当空间尺度由32 m递降到992 m，两种尺度转换误差的绝对值均值由0.15%左右增加到1%左右，误差绝对值的最大值由约1.5%增加到5%左右。且局部高动态活跃水体，其空间尺度误差可达到10%左右，但所占整体区域比例较小，因此本研究未重点讨论。

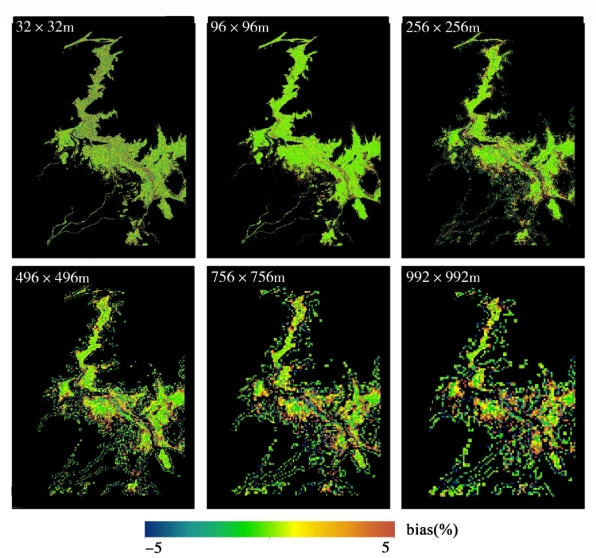
图5-20　基于悬浮颗粒物产品像元平均法与点扩散函数法的鄱阳湖悬浮颗粒物反演误差趋势分布图

对比分析图5-19和图5-20的两种空间尺度转换方法的误差分布趋势图，结合图5-21和图5-22的两种方法的误差统计直方图，可以得出以下结论:第一，基于遥感反射率数据(PSF-RRS)的空间像元平均法的水环境遥感产品的误差水平整体要优于基于悬浮颗粒物产品(PSF-TSS)的像元平均法的产品，表现为在多个尺度转换过程中，前者的相对偏差更趋近于0，且偏差直方图的分布更集中，误差的动态范围更小。如在空间尺度为32，256，496和756 m时，基于悬浮颗粒物产品(PSF-TSS)的像元平均法误差的最高值和动态范围都远大于基于遥感反射率数据(PSF-RRS)的空间像元平均法。第二，基于悬浮颗粒物产品(PSF-TSS)的像元平均法误差的均值随着空间尺度下降而增大的速率大于基于遥感反射率数据(PSF-RRS)的空间像元平均法，即PSF-TSS方法引起的误差会随着空间尺度的降低而快速增大。

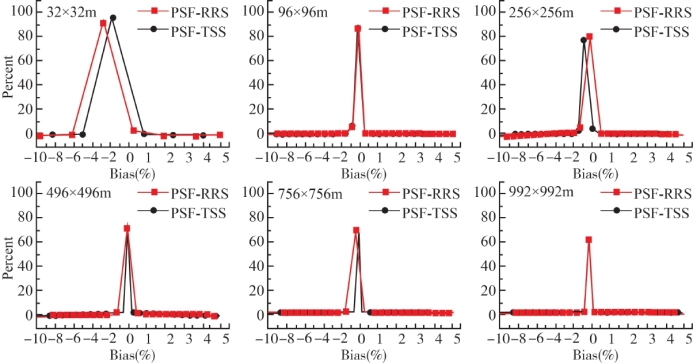
图5-21　基于遥感反射率数据(PSF-RRS)和基于悬浮颗粒物产品(PSF-TSS)

像元平均法与点扩散函数法的鄱阳湖悬浮颗粒物反演误差统计直方图

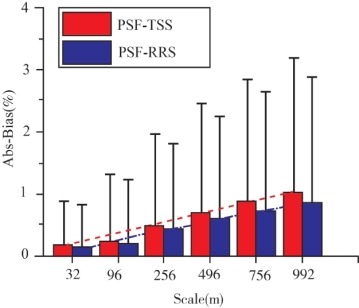
图5-22　基于遥感反射率数据(PSF-RRS)和基于悬浮颗粒物产品(PSF-TSS)

像元平均法的误差趋势图

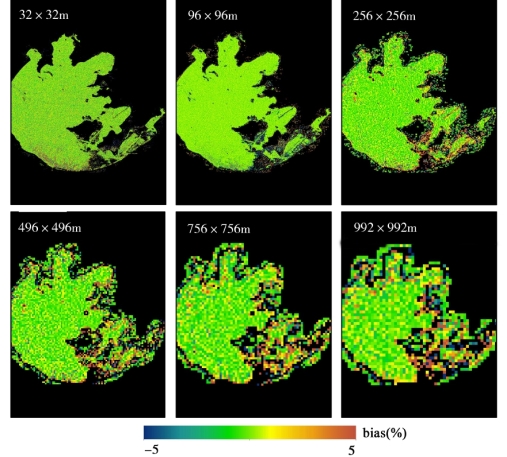
图5-23　基于遥感反射率数据像元平均法与点扩散函数法的太湖悬浮颗粒物反演的误差趋势分布图

(www.daowen.com)

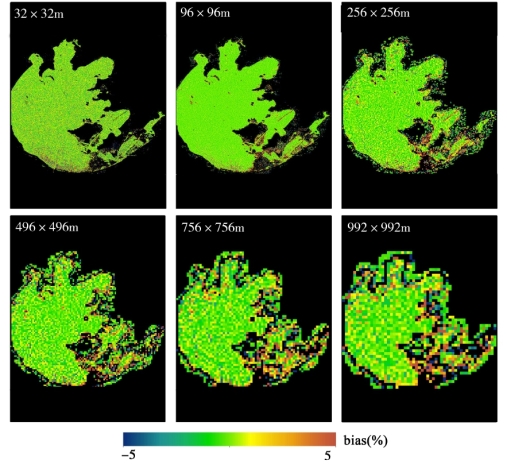
图5-24　基于悬浮颗粒物产品像元平均法与点扩散函数法的太湖悬浮颗粒物反演的误差趋势分布图

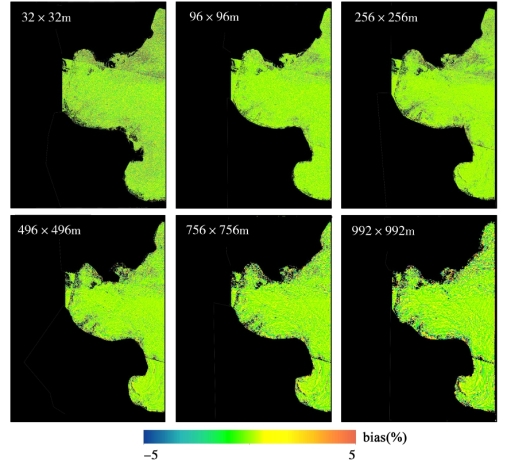
图5-25　基于遥感反射率数据像元平均法与点扩散函数法的渤海湾悬浮颗粒物反演的误差趋势分布图

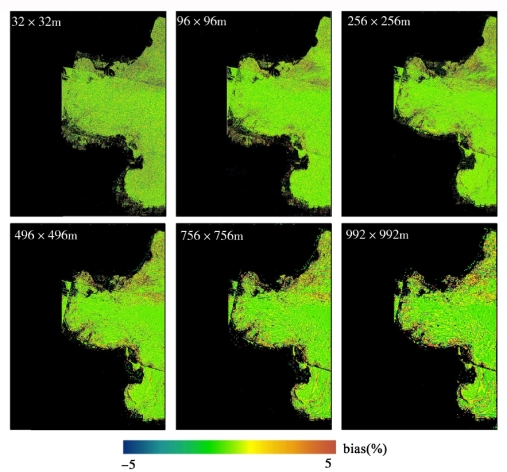
图5-26　基于悬浮颗粒物产品像元平均法与点扩散函数法的渤海湾悬浮颗粒物反演的误差趋势分布图

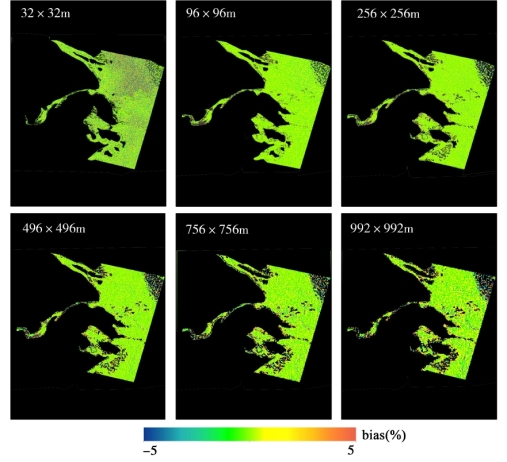
图5-27　基于遥感反射率数据像元平均法与点扩散函数法的长江口悬浮颗粒物反演的误差趋势分布图

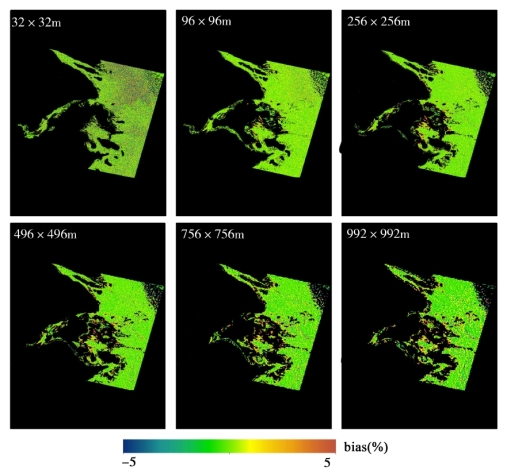
图5-28　基于悬浮颗粒物产品像元平均法与点扩散函数法的长江口悬浮颗粒物反演的误差趋势分布图

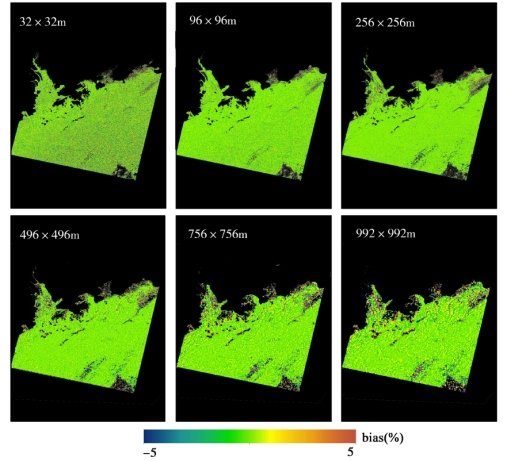
图5-29　基于遥感反射率数据像元平均法与点扩散函数法的珠江口悬浮颗粒物反演的误差趋势分布图

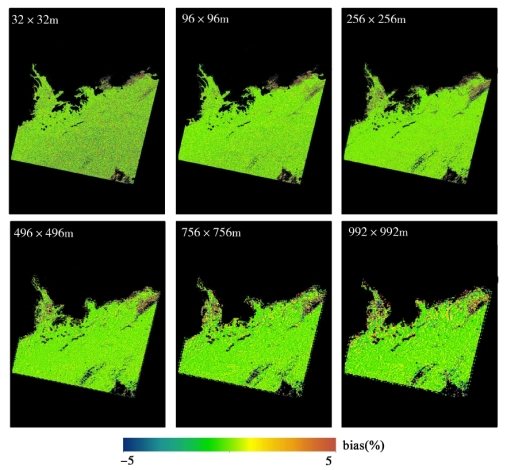
图5-30　基于悬浮颗粒物产品像元平均法与点扩散函数法的珠江口悬浮颗粒物反演的误差趋势分布图

基于上述的分析理论和方法，本研究分别对其他4个典型的近岸/内陆区域，包括太湖(图5-23和图5-24)、渤海湾(图5-25和图5-26)、长江口(图5-27和图5-28)、珠江口(图5-29和图5-30)水环境的空间尺度转换和空间尺度误差问题进行了探讨。与鄱阳湖空间尺度误差分布和趋势的结果类似，上述4个高动态浑浊水体区域表现出较显著的空间尺度误差问题，且两种空间尺度转换方法引起悬浮颗粒物产品的误差随着空间尺度的降低而增大。在近岸、河流入口等水环境时空变化特征较显著的区域，空间尺度误差较大。同样，基于遥感反射率数据(PSF-RRS)的空间像元平均法的水环境遥感产品的误差水平整体要优于基于悬浮颗粒物产品(PSF-TSS)的像元平均法的产品。

为了对比近岸/内陆水体的高动态空间变异特性引起的空间尺度问题，本研究同时以南海海域相对平静的水体进行了上述空间尺度和尺度误差问题的探讨。图5-31和图5-32为两种空间尺度转换方法的误差分布趋势图，结合两种方法的误差统计直方图5-33和图5-34，可以得出:针对南海水体，采用两种空间尺度转换方法引起的悬浮颗粒物产品的空间尺度误差均相对较小，整体的误差水平均小于±1 %；两种方法虽然存在一定误差水平的差异，但整体结果比较一致，其误差绝对值的平均值均小于0.2%，并且误差水平随空间尺度下降而变化的趋势不明显，只有在空间分辨率降低到992 m的时候，空间尺度误差才由较稳定的0.05%升高到0.12%。

图5-31　基于遥感反射率数据像元平均法与点扩散函数法的南海悬浮颗粒物反演的误差趋势分布图

图5-32　基于悬浮颗粒物产品像元平均法与点扩散函数法的南海悬浮颗粒物反演的误差趋势分布图

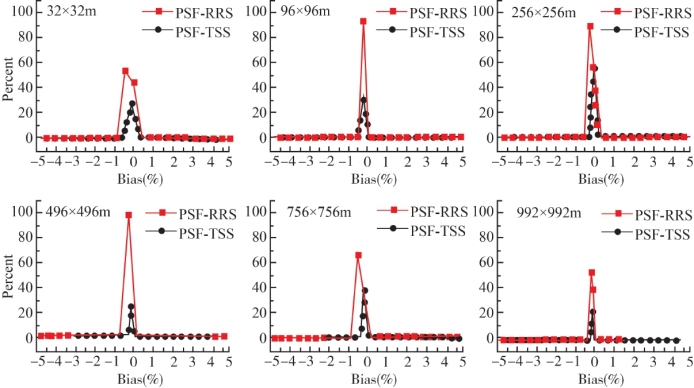
图5-33　基于遥感反射率数据(PSF-RRS)和基于悬浮颗粒物产品(PSF-TSS)像元平均法

与点扩散函数法的南海悬浮颗粒物反演误差统计直方图

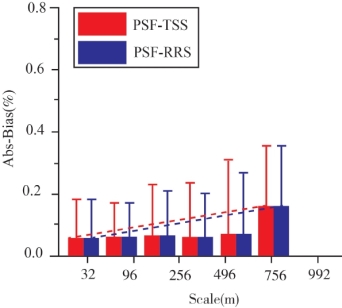
图5-34　基于遥感反射率数据(PSF-RRS)和基于悬浮颗粒物产品

(PSF-TSS)像元平均法的误差趋势图

相对以鄱阳湖为典型代表的近岸/内陆高动态水体，在本研究的空间尺度变化范围内，由尺度差异引起的水环境定量产品差异在南海等类似平静海水区域可以忽略不计。而对于鄱阳湖等二类浑浊水体，由于其较活跃的水环境特性，空间尺度变化引起的产品误差可能超过±5%，并最大到达±10%左右。因此，考虑到水环境定量遥感和水环境监测高精度发展和应用的需求，在多源多空间尺度遥感数据综合应用的背景下，空间尺度及尺度误差问题的研究具有重要意义。