遥感影像观测尺度或者空间分辨率决定了遥感数据所获得的最小空间变异单元，小于遥感观测空间尺度的地表参数变异无法被有效解析。最佳空间尺度的大小与地理要素自身的空间变异特征有潜在的关系，因此，如何定量化描述地球系统过程和现象的空间特征是空间尺度研究的关键之一。遥感影像的最佳空间尺度或者空间分辨率，受所研究的地理要素的内在空间特征和研究需求的影响。随着遥感影像空间分辨率的降低和地物目标本身空间异质性的增加，由遥感参数反演模型的非线性和不均一像元引起的，遥感反演获取的地表参数产品存在典型的尺度效应(Chen，1999；陈军等，2008)。针对水环境尺度效应的研究也已经证明了由于遥感空间分辨率的不足，造成了对全球水色产品统计和分析的低估(Lee，Hu et al.，2012；陈军等，2010)。由于过低或者过高的空间分辨率分别会造成空间信息监测能力的不足或者信息的冗余，数据存储、处理、分析的资源浪费，因此，根据地表要素的典型空间变化特征，研究其最优空间监测尺度具有重要意义。

基于空间统计学空间自相关理论的遥感影像尺度问题研究方法是目前应用较为广泛的一种方法。依据空间上邻近的地物之间的相关程度要强于空间上距离较远的地物的基本地理学基本规律，Woodcock和Strahler提出的局部方差(local variance)方法(Woodcock and Strahler，1987)，Markowitz提出的半方差(semivariance，也称为变异函数)方法(Markowitz，1968)。半变异函数是定量化描述空间依赖性和异质性的一个综合性指标。通过循环计算研究区域内由特定空间距离间隔的同一地表要素变量的差异，获取多种尺度上对区域化随机变量的变异性量度。

经验性半变异函数的计算公式如公式(5-1)所示，r(h)为区域化半变异函数值，z(x)为地理要素在位置x处的变量值，z(x+h)是与位置x相距h的地理要素的变量值，N(h)为相距h的点对数目。r(h)表征了半变异函数的经验估计值，通过最小二乘法实现非线性拟合(公式(5-2))。即可得到半变异函数的理论模型(公式(3-3))，常用的拟合模型有球状模型、指数模型、高斯模型，本研究根据数据情况和经验，选择使用较为通用的球状拟合模型。

经验半变异函数:

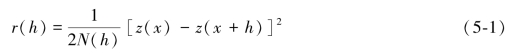
拟合半变异函数:

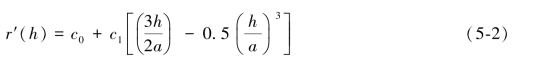(www.daowen.com)

最小二乘法:

图5-1给出了一个经验半变异函数和拟合的理论模型结果示意图。拟合的理论模型提供了可定量化描述空间变异的三个重要参数:变程a(range)、块金值C0(nugget)和基台值C0+C1(sill)。变程a表征了地理要素的空间变异尺度，空间距离大于变程a的地理变量将不具有空间相关性，即空间异质性会对统计结果产生影响。块金值C0表示在当前空间尺度下，由于空间内变异引起的不能被解析的空间变化信息，即小于当前观测尺度的空间变异特征。基台值C0+C1表征了研究区域的整体空间最大变异程度。

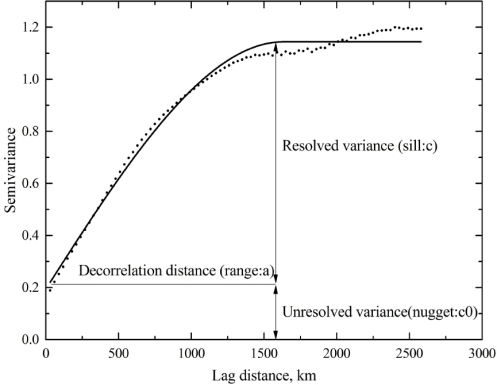
图5-1　经验(点)和拟合(实线)的半变异函数示意图