音乐家大多数对数学不感兴趣，他们对这门学科敬而远之。但是，那些如同普希金笔下的萨利埃里还没有“用代数检验过和声”的音乐家们，接触到数学的次数远远超过了他们的想象，而且还是对数这么“高深度”的内容。

为了证明这一点，我们看一下一位已故的物理学家说过的一段话：

“我的一位中学同学喜欢弹钢琴，但是不喜欢数学。他还说过这样的话，音乐和数学之间没有任何关系。不过，毕达哥拉斯发现了声音和振动之间的关系，但他眼中的音阶不适用于我们的音乐。你可以想象，当我告诉我的同学，他在弹现代钢琴的琴键时就是在弹对数，他是如何的震惊，又是如何的难以置信。”

事实的确如此，等音程半音音节中的“音程”不是按照声音的频率、波长设置的，而是按照这些数量的对数设置的。只是这种对数的底数不是通常情况下的10，而是2。

最低的八音度，也就是我们所说的零八度音，如果其中的音do每秒钟振动的次数是n，那么，第一个八度音的do每秒钟将会振动2n次，第m个八音度的do每秒钟振动n×2m次。把第一个八度音的基音do当作0，钢琴上半音音阶里的任意一个音为p，那么，第七个音是sol，第九个音就是la，以此类推。由于等音程半音音阶里每一个后面的一个音的频率是前面一个音的频率的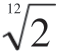 倍，所有任意一个音（第m八度音里面第九个音）的频率可以表示为：

上面等式的两端同时取对数，得到：(www.daowen.com)

或者写成：

将最低的音do每秒钟振动的次数定为1（也就是n=1），把以2为底数的对数进行转换（或者取log2=1），得到：

由此可知，钢琴上琴键的序号就是相应音调的频率的对数^[5]。我们也可以这样说，表示八度音的那个号码m就是对数的首数，而表示音调在这个八音度的次序的p^[6]就是对数的尾数。里面，数3是这个音的频率以2为底数的对数的首数，而是对数的尾数。因此，音频是最低八音度中的音do的

例如，八度音里的第三个音sol，在频率的23.583倍，也就是11.98倍。