题：桌子上有一支点燃的蜡烛，还放着一枚硬币，请问：当蜡烛的烛焰距离桌面多高时硬币被照得最亮？

解：有些人可能会觉得烛焰越低，硬币被照得越亮，因此只要把蜡烛放到最低就可以了。实际上并非如此，烛焰太低时，光线会斜得很厉害；而烛焰太高时，光线又是垂直的，硬币离光源会变远。显然，为了使硬币被照得最亮，烛焰应该处于某一个高度。设烛焰A 到桌面的距离是x，垂足是C，点C 到硬币B 的距离是a（图7-14）。如果烛焰的亮度是i，根据光学定律可知，硬币处的亮度可以表示为：

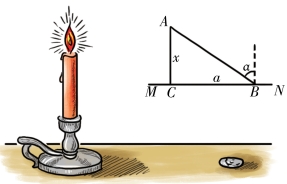
图7-14

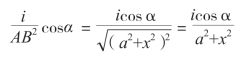
α 指的是光线AB 的投射角。因为：

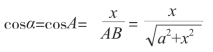
所以，硬币的亮度是：

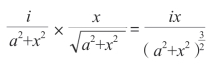
把等式右边的表达式平方得到：

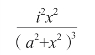
当它的值最大时，平方前的表达式的值也最大。

i2 是一个常数，可以略去不计。表达式的剩余部分可以变化成：

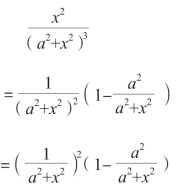
当上面的表达式的值最大时，表达式：(www.daowen.com)

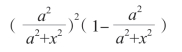
的值也最大。因为后面的表达式加入了a4 这个乘数，而它是一个常数，不会影响乘积最大时x 的取值。我们经过观察得知，上面两个乘数的底数之和：

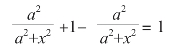
是一个常数。因此，我们得到这样的结论，当：

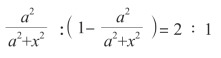
时，所讨论方程的乘积的值最大。

由上面的比例关系，得到方程：

2x2+2a2-2a2=a2

解方程得到：

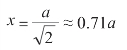
所以，当烛焰到桌面的距离是硬币到蜡烛投影的水平距离的0.71 倍时，硬币被照得最亮。知道了这一比例关系，我们在工作中就能充分利用最佳照明的效果。

【注释】

[1]在这里k 的值大于零，因为0.8m=a-x+4＞a-x+x=a。