题：有一块矩形的金属片（图7-9），要用它做一个槽，截面是一个等腰梯形，可以做成各种样子（图7-10）。请问：各个面应该多宽，折成多少度的角（图7-11）才能使这个槽的截面的面积最大？

图7-9

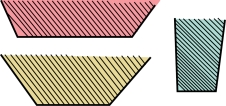
图7-10

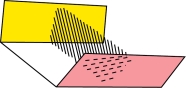
图7-11

解：设矩形金属片的宽是L，被折起的侧面的宽度是x，底面的宽度是y。我们还要引入另一个未知数z，它的意义如图7-12 所示。

槽的梯形截面的面积是：

这道题的问题是当x、y、z 的值是多少时，面积S 的值最大。因为（2x+y）等于矩形金属片的宽度L，我们把上面的等式变形为：

S2=（y+z）2（x+z）（x-z）

当S2 取得最大值时，3S2 的值也最大，而3S2 用乘积的形式表示出来是：

（y+z）（y+z）（x+z）（3x-3z）

这四个乘数的和是：

（y+z）+（y+z）+（x+z）+（3x-3z）=2y+4x=2L(www.daowen.com)

这是一个确定的值。所以，只有当四个乘数都相等的时候，也就是：

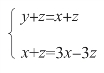
时，它们的乘积才最大。

从第一个方程中得到：

y=x

因为y+2x=L，所以上面的等式变为：

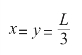
从第二个方程中得到：

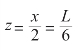
在直角三角形中（图7-12），由于直角边z 是斜边x 的一半，因此直角边z 所对的角度是30°，而槽的底面和斜面的夹角是：

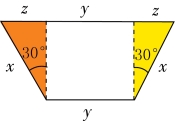
图7-12

90°+30°=120°

所以，当这个槽的侧面折成半个正六边形的三个邻边的形状时，才能使这个槽的截面的面积最大。