题：把一栋旧房子拆除后，只剩下一面完整的墙。现在，想要在这个旧址上建一栋新房。已知：剩下的墙的长度是12 米，新房的面积是112 平方米，修缮1 米长的旧墙的费用是砌新墙费用的25%，用拆旧墙所得的材料砌新墙时1 米的花销是用新材料砌新墙的50%。在这种条件下，如何利用这面旧墙最合理？

解：假设保留的旧墙的长度是x 米，新房面积的宽为y 米，那么，旧墙中被拆除的部分就是（12-x）米，得到的材料用来建新房的墙体（图7-7）。如果用新材料砌每米新墙的费用是a，那么，修缮x 米旧墙的费用就是，用旧料来重建（12-x）米新墙所需的费用是，这面墙其他部分的花费是a[y-（12-x）]，即a（y+x-12）。第三面墙需要的费用是ax，第四面墙的费用是ay。所以，整个工程需要的费用是：

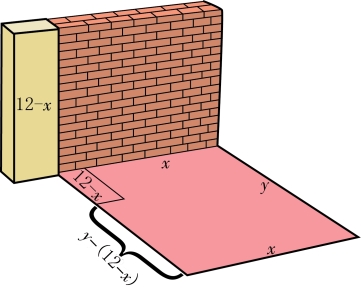
图7-7

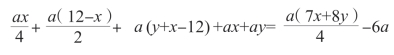
当（7x+8y）的值最小时，上面的表达式的值也最小。因为新房的面积xy的值是112，所以：

7x×8y=56×112

由于7x 和8y 的乘积是一个常数，所以当7x=8y 的时候，它们的和最小。此时：

(www.daowen.com)

将y 的值代入方程：

xy=112

得到：

解方程得到：

由于旧墙的长度是12 米，因此只要拆掉0.7 米就行了。