题：城市A 是一个滨河城市，在它下游a 千米的地方是城市B，城市B 到河岸的距离是d 千米（图7-4）。现在要从城市A 往城市B 运货，已知水路运费是公路运费的一半（按照每吨千米计算），为了使A 到B 的运费最低，从B到河岸的公路BD 要如何修建？

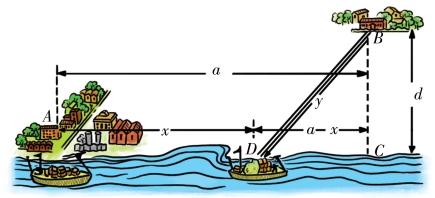
图7-4

解：设AD 之间的距离是x，公路BD 的长度是y，所需运费的最小值是m。由题意可知，AC 的距离是a，BC 的距离是d。因为运费和路程是正比关系，所以列出方程：

x+2y=m

由于x=a-DC，，于是，方程可以变形为：

去掉根号后得到：

3y2-4（m-a）y+（m-a）2+d 2=0(www.daowen.com)

求得：

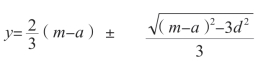
为了使y 是一个实数，（m-a）2 不能小于3d2。因此，当（m-a）2=3d2 时，（m-a）2 的值最小。那么：

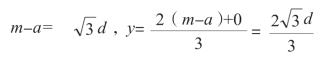
由于sin ∠BDC=d÷y，也就是：

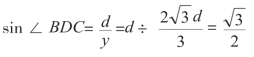
正弦sin对应的角度是60°，也就是说，无论a 的距离多长，修建的公路都要和河流成60°的角。

这道题的解和前面那一道题的解类似，只有在特定的条件下才成立。如果修建的公路BD 和河流之间的角度是60°，但是在城市A 的另一侧，这个解就不合适了。因为在这种情况下，修建从A 到B 的公路就可以了，根本不需要再走水路。