格丹诺夫·别尔斯基的名画《难题》（图6-3）众所周知，但很少有人去研究画上的难题。这道题的难点在于，用口算快速地说出这个式子的得数：

图6-3

这道题确实不容易口算出来，但对于一位特殊的教师教出来的学生却易如反掌。这位特殊的教师就是画中的那位——大学教授拉钦斯基，他离开自己的自然科学研究室，去乡村当了一名普通的教师。这位天才教师在学校推行口算，让学生熟练地掌握某些数的特征。例如，10、11、12、13、14这五个数就有一个有趣的特征：

102+112+122=132+142

由于100+121+144=365，因此很容易得出画中难题的答案是2。

代数可以让我们提出更多的关于这种数列的问题。

除了上面的例子，是否还有其他的五个数具备这种特征，前面三个数的平方和等于后面两个数的平方和？

解：设所求的数列中的第一个数是x，列出方程：

x2+（x+1）2+（x+2）2=（x+3）2+（x+4）2(www.daowen.com)

不过，用x 表示数列中的第二个数会更好，这样方程会简单得多：

（x-1）2+x2+（x+1）2=（x+2）2+（x+3）2

化简方程得到：

x2-10x-11=0

解方程得到：

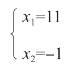
因此，有两组数列具有题中所要求的特征，除了拉钦斯基那一组，还有一组是：

-2、-1、0、1、2

也就是：

（-2）2+（-1）2+02=12+22