在上一道题中，我们找到了两组扬声器声音强弱相同的点，使用相同的方法，我们也可以找到地球和月球这两个天体对火箭的引力相同的点。现在，我们来寻找一下这样的点。

由牛顿定理可知，两个物体的质量和它们之间的引力是正比关系，距离和引力是反比关系。如果地球的质量是M，火箭和地球之间的距离是x，那么，地球对每克火箭的引力是：

k表示的是两个质量是1克的物体相距1厘米时相互之间的引力。

月球对每克火箭的引力是：

m表示的是月球的质量，l是月球到地球的距离（假设火箭不仅位于地球和月球之间，还在它们的连线上）。根据题意列出方程：

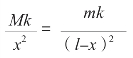
化简方程得到：

由天文学知识可知，≈81.5，将数值带入上面的方程中得到：

方程变形后是：

80.5x2-163lx+81.5l2=0

解方程得到：(www.daowen.com)

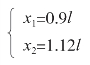
和上面那道关于扬声器的题类似，我们可以得到这样的结论：在连接地球和月球的直线上存在两个对火箭引力相同的点，一个点是到地心的距离是地球到月球的距离的0.9 倍，另一个点是地月距离的1.12 倍。由于地球到月球的距离大约是384 000 千米，因此两个点到地心的距离分别是346 000 千米和430 000 千米。

从上题中我们得知，以两点之间的距离作为直径的圆上的点都具有这种性质。让这个圆绕着连接地球和月球的直线旋转，就会形成一个球面，而且球面上的每个点都满足地球和月球对火箭的引力相同这一条件。

这个球确定了月球的引力范围（图6-2），球的直径为：

图6-2

1.12l-0.9l=0.22l≈84 000千米

一直以来许多人这样认为，火箭进入了月球的引力范围，就可以到达月球。也就是说，只要进入了这个范围，不管火箭的速度如何，都能够降落到月球上，因为这里月球对物体的引力大于地球对物体的引力。如果真是如此，那登月就简单多了，因为这时要克服的困难不是瞄准直径在天空中只有1/2 度视角的月球，而是瞄准直径为84 000 千米，有着12 度视角的球形区域。

很明显，这种想法是错误的。

假设从地球上发射一支火箭，随着地球引力的变化火箭的速度不断减小，当进入月球引力的范围时，火箭的速度正好降为零。那么，这支火箭能降落到月球上吗？答案是绝对不可能。

第一，即使在月球的引力范围内，地球的引力依然在起作用。因为在地心和月心的连线之外，月球的引力和地球的引力按照平行四边形的法则形成了一种合力，而且这种合力没有指向月球（只有在地球和月球的连线上，合力才指向月心）。

第二，月球一直处于运动之中，并不是静止不动的。如果我们想知道火箭是否会降落到月球上，就要考虑火箭相对于月球的运行速度。因此，想要让月球把火箭吸引到自己身边，或者把火箭当作卫星控制在自己的引力范围内，那么，火箭相对于月球的运行速度要足够大才可以。

其实，在火箭还没有进入月球的引力范围时，月球的引力就开始影响火箭的运行速度了。火箭在太空中运行的时候，从它进入所谓的月球影响范围——半径为66 000 千米的区域，才开始考虑月球的引力问题。这时来分析火箭相对于月球的运行状况，虽然可以忽略地球的引力，但是要计算出火箭相对于月球的运行速度。因此，在设计火箭的运行轨道时，必须使火箭进入月球的引力范围后，仍然有足够大的速度使它飞向月球。由此可以得知，火箭到达月球并不容易，更不像进入直径为84 000 千米的球形区域那么简单。