了解了乘方的逆运算，我们来看下面代数学中的两幕滑稽剧：2=3和2×2=5。很明显，大家一看就知道这两个等式是错误的，但它们是怎么得出来的呢？下面，我们来演示一下。

第一幕滑稽剧：

2=3

首先，“舞台上”会出现一个正确的等式：

4-10=9-15

接着，等式两边同时加上，等式变形为：

然后，就开始了下面的变形，滑稽剧的剧情也跟着变化：

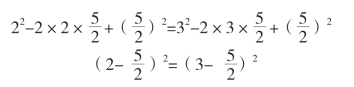
等式两边同时开方，得到：

在等式两边同时加上，得到：

2=3

那么，究竟是哪个环节出现了错误呢？

解：错误是：

是正确的，但推导出来的

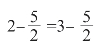
不正确。因为两个数的平方相等，这两个数不一定相等。例如：（-4）2=42，但-4≠4。两个数互为相反数时，它们的平方相等，上面的例子就是这种情况：

(www.daowen.com)

但是，绝对不等于。

第二幕滑稽剧（图5-1）：

图5-1

2×2=5

也按照上一幕的剧情往下演，先给出一个完全正确的等式：

16-36=25-45

在等式的两边同时加上一个数

，将得到一个新的等式：

将等式变形为：

将等式两边同时开方，得到：

在等式两边同时加上，得到：

4=5

就出现了开始时的2×2=5。

解：这与第一幕滑稽剧的错误是相同的是正确的，但推导出来不正确。