三个整数的三次方的和可能是另一个整数的三次方。例如：

33+43+53=63

也可以这样说，边长分别是3厘米、4厘米和5厘米的正方体的体积和等于边长是6厘米的正方体的体积（图4-4）。

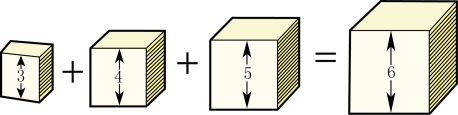
图4-4

接下来，我们看看其他的满足这种关系的等式，也就是求解方程：

x3+y3+z3=u3

我们用-t表示u，方程将变为：

x3+y3+z3+t3=0

我们来分析一下，有什么办法能够解出这个方程。假如a、b、c、d和α、β、γ、δ是方程的两组解。把第二组解中的四个数扩大k倍，然后和第一组解中的四个对应数相加，但k的值要使相加后的各数

a+kα，b+kβ，c+kγ，d+kδ

满足上面的方程。也就是说，k的值要满足下面的等式：

（a+kα）3+（b+kβ）3+（c+kγ）3+（d+kδ）3=0

因为a、b、c、d和α、β、γ、δ 是方程的两组解，所以有下面的等式：

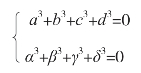
因此，等式（a+kα）3+（b+kβ）3+（c+kγ）3+（d+kδ）3=0化简后得到：

3k [（a2α+b2β+c2γ+d2δ）+k（aα2+bβ2+cγ2+dδ2）]=0

上面等式左边的两项至少有一项是零时，乘积才会是零。分别令这两项为零，我们将会得到两个k 值。一个是k=0，我们不研究这个值，因为这意味着a、b、c、d 不加任何数满足方程。因此，我们来看第二个值：

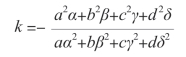
由此可知，如果知道满足方程的两组解，就可以求出另一组新的解。这组新解的求法是：用第二组解中的四个数分别乘以上面的k值，然后和第一组解中的四个对应数相加就可以了。

要使用这种方法，就必须知道方程的两组解。我们已经知道一组解是（3，4，5，-6），如何找出另一组解呢？假设第二组解中的四个数是r，-r，s，-s，显然，它们满足最初的方程。令：

a=3，b=4，c=5，d=-6；

α=r，β=-r，γ=s，δ=-s

因此，k的值为：

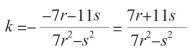
而a+kα，b+kβ，c+kγ，d+kδ对应的值是：

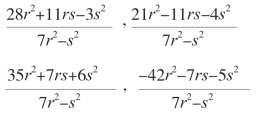
上面的四个表达式满足方程x3+y3+z3+t3=0，由于分母都相同，可以消去。也就是说，四个分子也满足x3+y3+z3+t3=0这个方程。因此，下面的四个数是方程的解：

x=28r2+11rs-3s2(www.daowen.com)

y=21r2-11rs-4s2

z=35r2+7rs+6s2

t=-42r2-7rs-5s2

为了证明这一点，可以把上面的数先进行三次方，然后再相加。假设赋予r、s 不同的值，我们就能得到方程一系列的解。当解中有公因数时，可以除以公因数。例如，r=s=1 时，我们求出x、y、z、t 的值分别是36、6、48、-54，也可以用它们除以公因数6，得到6、1、8、-9这四个数。因此：

63+13+83=93

下面是r和s取不同的值时，得到的一系列等式（除以公因数化简后的）：

r=1，s=2：383+733=173+763

r=1，s=3：173+553=243+543

r=1，s=5：43+1103=673+1013

r=1，s=4：83+533=293+503

r=1，s=-1：73+143+173=203

r=1，s=-2：23+163=93+153

r=2，s=-1：293+343+443=533

…

我们发现，如果把一组解中的四个数的位置调换一下，使用方法不变，就可以得到一组新的解。例如，把第一组解中的3、4、5、-6变为3、5、4、-6（即a=3，b=5，c=4，d=-6），这时x、y、z、t的值分别是：

x=20r2+10rs-3s2

y=12r2-10rs-5s2

z=16r2+8rs+6s2

t=-24r2-8rs-4s2

当r和s取不同的值是，由此得到一系列新的等式：

r=1，s=1：93+103=13+123

r=1，s=3：233+943=633+843

r=1，s=5：53+1633+1643=2063

r=1，s=6：73+543+573=703

r=2，s=1：233+973+863=1163

r=1，s=-3：33+363+373=463

…

由此可知，用上述方法可以求得方程的无数组解。