在地面上画垂线有一个简单的方法：任意选一点A，过点A作直线MN，从点A沿AM方向取任意距离a的三倍，终点是B。然后找一条绳子，打上三个结，相邻两个结之间的距离是4a和5a。接着将绳子两端的结固定在点A和点B处，拉紧中间的结（点C）。这样，就构成了一个直角三角形，角A是直角。（图4-3）

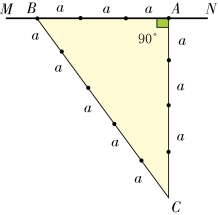
图4-3

这是一个古老的方法，几千年前在修建金字塔的时候，建筑师就使用过这个方法。它的理论依据是：在三角形中，当它的三条边的比例是3∶4∶5 时，由勾股定理可知，这个三角形是直角三角形，因为：

32+42=52

大家知道，除了3、4、5，还有很多其他的正整数a、b、c满足这种关系：

a2+b2=c2

这些数字叫作“勾股数”（也称毕达哥拉斯数）。根据勾股定理可知，这些数可以构成直角三角形的三条边，a和b是直角边，c是斜边。

显然，如果a、b、c是一组勾股数，它们乘上一个整数p后，pa、pb、pc也是一组勾股数。反之，如果一组勾股数有一个公因数q，它们除以q后，还是一组勾股数。因此，我们只讨论互为质数的勾股数（因为其他的勾股数是它们乘上p得到的）。

我们知道，在勾股数a、b、c中，两个直角边一个是偶数，另一个是奇数。现在，我们用反证法来证明这个结论是否正确。

如果直角边a和b都是偶数，那么，（a2+b2）也一定是偶数，这就意味着斜边也是偶数。也就是说，a、b、c至少有一个公因数2，和a、b、c互为质数相矛盾。因此，必须有一个直角边是奇数。

还有一种可能，两个直角边都是奇数，斜边是偶数。很容易证明，这种假设是错的。如果直角边是（2x+1）和（2y+1），它们的平方和是：

4x2+4x+1+4y2+4y+1=4（x2+x+y2+y）+2

也就是说，斜边的平方除以4后余数是2。但是，任意一个偶数的平方都能够被4整除。也就是说，斜边不是偶数，假设不成立。

因此，在直角边a和b中，其中一个是奇数，另一个是偶数。因此，（a2+b2）是奇数，这意味着斜边也是奇数。

如果直角边a是奇数，直角边b是偶数，由勾股定理得出：

a2=c2-b2=（c+b）（c-b）

等式右边的乘数（c+b）和（c-b）互为质数。如果它们有一个公因数（1除外），那么，它们的和是：

（c+b）+（c-b）=2c

它们的差是：

（c+b）-（c-b）=2b

它们的乘积是：也就是说，2c、2b、a2有一个公因数。既然a是奇数，这个公因数一定不是2，所以a、b、c可能有一个公因数，但这是不可能的。因此，假设不是错误的，（c+b）和（c-b）一定互为质数。

（c+b）（c-b）=a2

如果互为质数的两个数的乘积是一个完全平方数，那么，这两个数也都是完全平方数，即

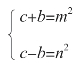
解方程组得到：

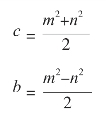(www.daowen.com)

所以：

a2=（c+b）（c-b）=m2n2，a=mn

于是，我们得到的正整数勾股数就是：

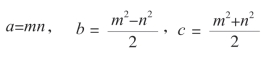
这里的m和n是互为质数的奇数。反过来，也很容易证明，当m和n是奇数时，一定能够找出勾股数a、b、c。

下面是m和n取不同的奇数时，得到的a、b、c（三个数都小于100）互为质数的所有的勾股数组：

m=3，n=1:32+42=52

m=5，n=1:52+122=132

m=7，n=1:72+242=252

m=9，n=1:92+402=412

m=11，n=1:112+602=612

m=13，n=1:132+842=852

m=5，n=3:152+82=172

m=7，n=3:212+202=292

m=11，n=3:332+562=652

m=13，n=3:392+802=892

m=7，n=5:352+122=372

m=9，n=5:452+282=532

m=11，n=5:552+482=732

m=13，n=5:652+722=972

m=9，n=7:632+162=652

m=11，n=7:772+362=852

勾股数还有其他的特征，我们只是列举出来，不再进行证明：

如果一条直角边小于3，另一条直角边小于4，那么，斜边将会小于5。

希望读者们利用上面的勾股数的特征，自己去验证一下。