谈到方程，就不能不提利用计算机解方程这个问题。前面我们已经讲过，计算机可以“下象棋”。另外，计算机还可以做其他的工作，例如，翻译语言、演奏乐曲等。

当然，我们不会研究“下象棋”和“语言翻译”的程序，因为这些程序太复杂了。我们只分析两个最简单的程序。在分析之前，我们先来看一下计算机的结构。

在第一章中我们就说过，有一种运算装置，一秒钟可以完成成千上万次运算，这个装置是计算机中的运算器。此外，计算机中还有控制器，调控计算机中的所有工作；存储器，也叫记忆装置，用来存放数据和预定的信号；输入和输出装置，输入新的数据及输出计算的结果。

大家都知道，把声音刻录到唱片上，就可以反复播放。不过，一张唱片只能录制一次，再想刻录就得换一张唱片。录音机的录制却不同，它是利用一种特殊胶带的磁性作用来录制的。录制之后不仅可以反复播放，还可以“抹掉”，录制其他的内容。一条磁带可以使用多次，当录制上新的内容之后，原来的内容就会“自动抹掉”。

计算机的存储器就是根据这个原理工作的。数据和预定的信号（借助于电信号、磁信号或机械信号）被刻录到磁带或者其他的装置上，需要的时候，这些数据和信号就会被“读”出来，不需要时就可以抹掉，再刻录新的内容。“记”和“读”这些数据和信号仅仅需要百万分之几秒的时间。

存储器由几千个单元组成，每个单元里都有几十个存储元件。假设二进制的存储是这样的：被磁化的元件表示1，没有磁化的元件表示0。比如，存储器的每个单元有25 个元件，该单元的第一个元件表示数的符号（正或者负），接下来的14 位用来存储数据的整数部分，剩下的10 位存储数据的小数部分。图2-8表示的是存储器的两个单元，每个单元含有25 个元件，用“+”表示被磁化的元件，“-”表示没有被磁化的元件。先来看一下上面那个单元，用虚线把符号位和数据隔开。这个单元中记录的数据是1011.01，也就是十进制的11.25。

存储器的单元不仅可以存储数据，还可以存储指令，而程序就是由指令组成的。我们分析一下，三地址的计算机的指令是由哪些部分组成的。这时，存储器单元要分成四段（图2-8下面的那个单元），第一段表示操作，操作是以数的形式（编码的形式）写入存储单元中的。例如：

加——操作Ⅰ

减——操作Ⅱ

乘——操作Ⅲ

除——操作Ⅳ

……

指令是这样表示的：单元的第一段表示操作码，第二段和第三段表示存储单元的编号（地址码），第四段存放所得结果的存储单元编号（地址码）。例如，图2-8的下行记录的二进制数是11、11、111、1011，也就是十进制中的3、3、7、11，表示的命令是：用位于第3 和第7 存储单元的数字完成操作Ⅲ的运算（乘法），把得到的结果存到第11 号存储单元中。

下面，我们直接以十进制的形式记录数据和命令。例如，图2-8可以记作：

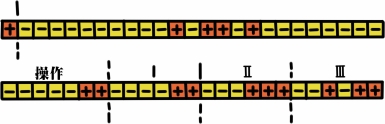
图2-8

乘 3 7 11

我们来看下面这一个程序：

（1）加 4 5 4

（2）乘 4 4 →

（3）转移 1

（4）0

（5）1

第一条指令：把存储器中第4 存储单元和第5 存储单元的数据相加，并把结果放到第4 存储单元中。由此可知，计算机第4 存储单元记录的数据是0+1=1。执行完第一条指令后，第5 存储单元中存储的数据不变，第4 存储单元中的数据由0 变成1。

第二条指令：对第4 存储单元中的数进行自乘运算，把结果12 输出（箭头表示输出）。

第三条指令：转移操作到第1 存储单元，也就是说返回去执行第一条指令。

第一条指令：把第4 存储单元和第5 存储单元的数据相加，并把结果放到第4 存储单元中。第4 存储单元中的数由1 变成2。

第二条指令：对第4 存储单元中的数进行自乘运算，把结果22 输出。

第三条指令：转移操作到第1 存储单元（又回到第一条指令）。

第一条指令：把数据2+1=3 存入第4 存储单元中，第4 存储单元中的数由2 变成3。

第二条指令：把第4 存储单元中数据3 自乘后输出。

第三条指令：转移操作到第1 存储单元中，等等。

我们发现，计算机在不停地计算整数的平方，并且把结果输出。我们不必输入新的数据，计算机会自己选出一个个整数，并把它们平方。计算机按照这个程序，在很短的时间内就能够算出1～10 000 中所有整数的平方。

需要说明的是，用计算机计算整数的平方的真正程序比上面的要复杂。第一个问题是针对第二条指令而言的，输出结果需要的时间比完成一道程序用的时间多得多。因此，计算机会把结果先储存到空闲的存储单元里，计算完成后再输出。上面的程序没有考虑到这个问题。

此外，计算机不能长时间进行平方运算，因为存储器的存储单元有限；在完成了我们所需要的运算后也无法及时停机，因为计算机每秒钟可以进行几千次的运算。因此，为了能够及时停机，需要一套特殊的指令。例如，在完成了1～10 000 中所有整数的平方后，计算机会自动停机。

在计算机中，计算1～10 000 中所有整数的平方的程序是这样的：

（1）加 8 9 8

（2）乘 8 8 10

（3）加 2 6 2

（4）条件转移 8 7 1

（5）停

（6）0 0 1

（7）10 000

（8）0

（9）1

（10）0

（11）0

（12）0

前面两条指令和我们上面所说的简单程序中的指令一样，执行完前两条指令后，第8、第9 和第10 存储单元中的数据将变为：

（8）1

（9）1

（10）12

第三条指令：把第2 存储单元和第6 存储单元中的数相加，结果放到第2存储单元中，第2 存储单元的数据变成：

（2）乘 8 8 11

可以看出，第三条指令完成后，第二条指令发生了变化，准确地说，存储结果的单元地址发生了变化，后面我们会解释出现这种情况的原因。

第四条指令：如果第8 存储单元的数小于第7 存储单元的数，就转移去执行第一条指令，反之，则执行下一条指令。现在，第8 存储单元中的1 小于第7 存储单元中的10 000，因此转移到第一条指令。

第一条指令完成后第8 存储单元中的数将会变成2。

第二条指令现在的形式是：

（2）乘 8 8 11

也就是说，把22 存储到第11 存储单元中。现在可以明白为什么要先进行第三条指令了，因为第10 个存储单元被占用了，所以应该把22 放到第11 个存储单元里。这时，有了下面的数据：

（8）2

（9）1

（10）12

（11）22(www.daowen.com)

执行完第三条指令后，第2 存储单元的形式是：

（2）乘 8 8 12

也就是说，计算结果将被储存到下一个单元中。因为第8 存储单元里的数依然小于第7 存储单元里的数，第4 条指令的意思是返回第一条指令。

执行完第一、二条指令后，我们得到：

（8）2

（9）1

（10）12

（11）22

（12）32

计算机会按照这个程序一直执行下去，那么，什么时候会停止呢？当第8存储单元里的数是10 000 的时候，算完了1～10 000 中所有整数的平方后。这时会执行第五条指令：停机，因为第8 存储单元里的数不再小于第7 存储单元里的数了。

接下来，我们来看第二个程序，求解方程组。我们要分析的是经过简化后的程序，如果读者感兴趣的话，可以试着写出完整的程序。

假设有一个方程组：

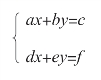
解方程得：

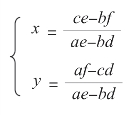
求解这样的方程组（a、b、c、d、e、f是常数），你最少要用几十秒的时间，而计算机一秒钟就能解出上千个这样的方程组。

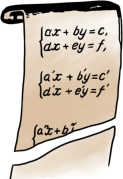
图2-9

我们来看下面这个程序，假设有几个这样的方程组：

（1）× 28 30 20 （14）+3 19 3 （27）b

（2）× 27 31 21 （15）+4 19 4 （28）c

（3）× 26 30 22 （16）+5 19 5 （29）d

（4）× 27 29 23 （17）+6 19 6 （30）e

（5）× 26 31 24 （18）转移 1 （31）f

（6）× 28 29 25 （19）6 6 0 （32）a'

（7）- 20 21 20 （20）0 （33）b'

（8）- 22 23 21 （21）0 （34）c'

（9）- 24 25 22 （22）0 （35）d'

（10）÷ 20 21 → （23）0 （36）e'

（11）÷ 22 21 → （24）0 （37）f '

（12）+1 19 1 （25）0 （38）a"

（13）+2 19 2 （26）a ……

第一条指令：把存储器中第28 存储单元和第30 存储单元的数据相乘，结果存储到第20 存储单元中。也就是说，把ce 放到第20 存储单元中。

依此执行第二到第六条指令，完成后，第20 存储单元到第25 存储单元中的数据是：

（20）ce

（21）bf

（22）ae

（23）bd

（24）af

（25）cd

第七条指令：用存储器第20 单元中的数据减去第21 单元中的数据，把结果（即ce-bf）存入第20 单元中。

依次完成第八、第九条指令，然后第20、21 和22 存储单元中的数据变成：

（20）ce-bf

（21）ae-bd

（22）af-cd

第十条和第十一条指令是做除法：

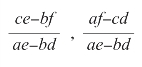
并把结果输出。这就是第一个方程组中x 和y 的解。

第十二到第十九条指令是解第二个方程组的，我们来分析一下计算机是怎么执行这些指令的。第十二条指令是把第1存储单元和第19存储单元中的数据相加，并把结果放到第1存储单元中。依次完成第十三到第十七条指令，这时第1存储单元到第6存储单元中的数据变成了：

（1）× 34 36 20

（2）× 33 37 21

（3）× 32 36 22

（4）× 33 35 23

（5）× 32 37 24

（6）× 34 35 25

第十八条指令：转移到第1 存储单元，也就是去执行第一条指令。

到此，前六个存储单元中的数据发生了什么变化呢？这些单元中的前两个地址的编码发生了变化，从26～31 变成了从32～37。也就是说，计算机还是在重复原来的计算，只是指令中第二和第三段中操作数的地址码发生了变化，不再从第26 存储单元到第31 存储单元中取数，而是从第32 存储单元到第37存储单元中取数。这样，计算机就解出了第二个方程组。依此类推，一直到解完所有的方程组为止。

上面的例子告诉我们，程序对于计算机是多么重要。因为计算机能够快速地完成各种运算，都是程序的功劳，离开这些程序，计算机什么也做不了。这些程序有求平方根的程序、对数据进行计算的程序、求三角函数的程序、解高次方程的程序，还有前面提到的下象棋的程序，语言翻译程序等。当然，问题的复杂程度决定了程序的复杂程度。

最后想要告诉大家的是，有一种编程程序，能够使计算机自动编写解题的程序，大大减轻了编程人员的负担。

【注释】

[1]长度单位，原指肘关节到中指尖的距离。

[2]这种关系只适用于铁皮不厚的罐头（严格来说，罐头的内外表面积不相等，而且罐头内外的高也是有差别的）。