题：有一天，爱因斯坦生病了，他的朋友莫希柯夫斯基为了帮他打发无聊的时间，出了这样一道题：

当分针和时针都指向12 的时候，把它们对调，它们所指示时间的位置是合理的，是存在的。但是，其他的时刻就不是这样了。例如，6 点时，把时针和分针对调，时间就不对了：当时针指向12 的时候，分针不可能指向6。那么，什么时间分针和时针可以对调，而且对调后的时间确实存在？

看完这道题，爱因斯坦说道：“这个问题很适合卧病在床的我，它不仅有趣还有一定的难度。不过，只怕打发不了多少时间，因为我快要解出来了。”

说完后，爱因斯坦坐起来，在纸上画了一个草图。不久，就把这道题解出来了……

大家想一下，这道题的答案到底是什么呢？

解：我们以表盘的为单位，表示表针从12 走过的距离。

假设走到了符合题中要求的位置，时针走了x 刻度，分针走了y 个刻度（图2-6）。由于时针每小时走5 个刻度，所以走x 个刻度需要的时间是小时。也就是说，在12 点之后，时针走了小时。分针每分钟走一个刻度，走y 个刻度需要小时。换言之，分针是在小时前走过数字12 的。或者说，分针和时针在12 点重合之后过了个小时。因为这里指的是12 点之后的整小时数，所以这个数是整数（0～11）。

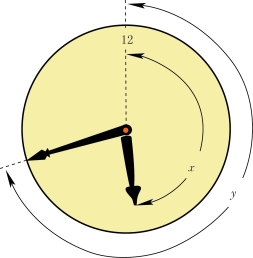
图2-6

表针对调之后，我们可以用上面的方法求出经过的时间是：

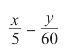
这个数也是整数。

联立方程组：

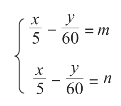
这里的m 和n 是0～11 的任意整数，由方程组得：(www.daowen.com)

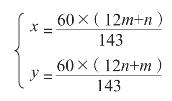
把0～11 的各个整数分别代入上面的方程组，就可以得出满足题意的表针的位置。因为代表m 的12 个整数可以和代表n 的12 个整数任意搭配，看起来有144 个解，但只存在143 个。因为m=n=0 和m=n=11 的时候，求出的是同一个时间。

当m=n=11 时，求得：

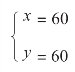
也就是说，m=n=0 时，也是12 点。

在这里，我们不一一讨论各种情况了，只列举两个具有代表性的例子。

例1：m=n=1 时，

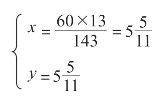
也就是1 点分，时针和分针重合，它们对调后还是原来的时间（其他的时针和分针重合的情况也一样）。

例2：m=8，n=5 时，

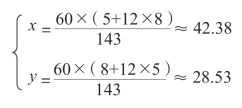
所指的时间是8 点28.53 分，对调后是5 点42.38 分。

我们已经知道了符合题意的答案有143 个，为了准确地表示出时针和分针的各种情况，需要把表盘平分成143 份，这样可以清楚地显示出各个答案。在其他的时间点，时针和分针不可以对调。