著名文学家托尔斯泰曾经提到过这样的一个问题：

题：有一队农夫去割草（图2-3），他们需要割完两块草地上的草，大块草地的面积是小块草地的两倍。前半天，大家都在大块的草地上割草。后来，一队农夫平均分成了两部分：一半人在原来的大块草地上割草，天黑时正好割完；另一半人去小块的草地上割草，天黑时剩下一小部分，第二天一个人去割草，一天的时间正好割完。

图2-3

请问：这队农夫有多少人？

解：设这队割草的农夫有x 人，每个人每天割草的面积是y。

用x 和y 表示大块草地的面积，x 个人半天所割草地的面积是：

剩余的部分是一半的人用半天的时间割完的，所以剩余的面积是：

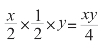
因为一天正好割完整片草地，所以草地的面积为：

接下来，用x 和y 表示小块草地的面积。一半的人割了半天，所割的面积是：

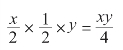
剩下的面积一个人一天正好可以割完，面积是y。所以，小块草地的总面积是：(www.daowen.com)

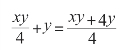
因为大块草地的面积是小块草地的两倍，可以得出：

方程两边同时除以，得到：

3x=2x+8

由此得知，x=8。

《趣味代数学》这本书刚出版不久，青格尔教授给我写了一封信，里面提到了这道题。他觉得，这道题的意义是：“它是一道简单的算术题，而不是一道代数题，难就难在它出现的形式，有别于通常的刻板形式。”

在信中，青格尔教授还说：“这道题是怎么来的呢？当时，我父亲和舅舅伊·拉耶夫斯基（列夫·托尔斯泰的密友）同时就读于莫斯科大学的数学系。在他们所学的课程中，有一门课类似于教学法，学生们需要去指定的市立民众中学学习相应的知识。我父亲和舅舅有一个叫彼得罗夫的同学，他喜欢研究算术学，经常有自己的独到见解。他觉得，算术课上的习题都是模式化的，解题的方法也是模式化的，对学生有百害而无一利。为了打破传统模式的桎梏，他自己发明了一套习题。由于这套习题太灵活，难倒了那些‘具有丰富经验的优秀教师们’。但是，那些头脑灵活的学生很容易就解出了这些习题。前面，我所提到的计算割草人数的这道题，就是其中的一个。借助方程，有经验的老师自然能解出这道题，他们却忽略了最简单的算术解法。”

其实，解这道题非常简单，没有必要列方程求解。

由于大块草地全队人割半天，半队人再割半天就可以割完，显然，半队人马半天割完草地的。那么，小块草地剩下的部分就是。也就是说，一个人一天割完草地的，当天割的总数是，由此可知，全队共有8 个人。

这道题是托尔斯泰当学生的时候，从我父亲那里听说的。后来，托尔斯泰一直很喜欢这类的题，既有趣又不难。等到我和托尔斯泰讨论这道题的时候，他已经是一个老者了。他发现，这道题通过画图（图2-4）会更清晰、更明了。

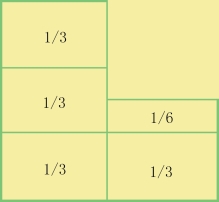
图2-4

接下来的几道题，用算术解比用方程解要简单得多。