6.4.1.1　SI 模型计算与分析

这里，以新安江水电站为例，依据1990～1999 年间的坝址地下水质分析资料，应用上述饱和指数模型首先进行区内坝踵帷幕体后地下水与某矿物之间反应状态的SI 计算，然后进行SI 的灵敏度分析，最后进行SI 的可信度分析。

根据对该时段水质资料系列的统计特征的检验（第五章表5.2.1），以水质有关变量的均值作为原始分析数据，通过模型计算，来反映该时段区内地下水与特定矿物之间的反应状态及其影响因素。

不失一般性，以右坝肩灌2-3 水质监测点的资料计算该部位的SI 值为例。考察如下化学反应式

（1）求离子强度I。对于灌2-3 孔位，有

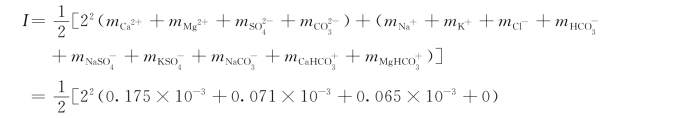
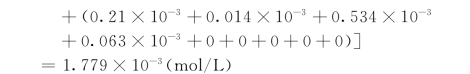
（2）求活度系数r。由于在灌2-3孔位，地下水的离子强度I＜0.1mol/L，故选用式（6.2.8）（Debye Hückel公式）分别计算地下水溶液中各单一离子和络阴离子的r 值。结果如下：

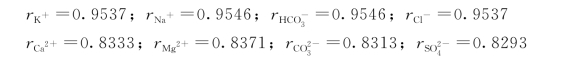
（3）计算主要化学组分及其衍生组分的浓度。根据式（6.2.10）～式（6.2.16），计算游离钠离子的浓度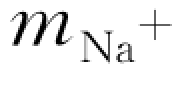，以及钠离子与其他组分反应所生成的络合物的浓度。根据同样的方法，可依次求出所有游离离子和相关络合物的浓度，有关计算结果见表6.4.1。

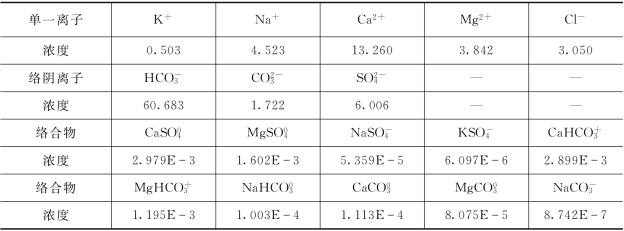
表6.4.1　灌2-3孔位宏量水化学组分的存在形式及其含量统计　单位：mg/L

（4）循环迭代至满足精度要求，并最终求出反映区内地下水与碳酸盐类物质之间反应状态的SI 值，其沿坝轴线的分布特征见图6.4.1。

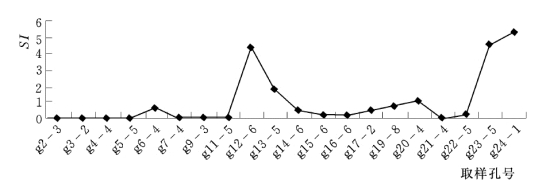
图6.4.1　坝基地下水监测点的SI 值沿坝轴线的分布曲线

根据数值计算结果，在沿坝轴线分布的20个水质监测点中，有15 个点的SI＜1，占75%；余5 个点的SI＞1，占25%。前者反映，相应部位地下水与碳酸盐类物质之间的反应状态呈非饱和态，表明相应水流系统中与水溶液相接触的此类固相物质处于继续被溶解的状态；而后者则反映，相应部位地下水与碳酸盐类物质之间的反应状态呈过饱和态，表明该部位溶解于水中的此类物质处于沉淀的状态。由图6.4.1 知，位于右坝肩的有关水质监测点位的SI 值普遍很小，如在灌3-2 孔位SI＝0.00082，反映出该部位的水溶液远离饱和态；而在位于河床及左坝肩的有关水质监测点位的SI 值明显大一些，其中有的点位的SI 值虽然小于1，但同右坝肩相比较，已相对接近于1。如在灌19-8孔位SI＝0.8010。现场调查发现，在灌浆廊道中位于河床及左坝肩的幕后排水孔口及其附近比较普遍地出现白色析出物，而在右坝肩部位此类白色胶状物质则不普遍。经对于样品的化学成分分析，其主要成分为CaO，结晶后则为CaCO3。显然，根据SI 的计算结果，在河床及左坝肩幕后不同排水孔位出现白色析出物具有两种不同的机制。即在SI＞1 的排水孔位，此类析出物主要是由于该部位地下水溶液（与碳酸盐类物质之间）呈过饱和态而析出；而在SI＜1 的排水孔位，出现此类析出物则由于孔口处水环境（如温度和压力等）的较大变化所致。同样，根据上述SI 的计算结果认为，右坝肩部分坝段地下水动态即使在对坝踵帷幕体进行了补强加固之后，仍然比较活跃。这是需要关注的。

6.4.1.2　SI 模型的灵敏度分析

在完成了对区内各水质监测点SI 值计算的基础上，进行该模型的灵敏度分析。

在分析过程中，设参数Pi 的变化量（即误差）为ΔPi，若参数Pi 为水质组分浓度时，则其变化量ΔPi 取其分析浓度的±1%、±2%、±3%、±4%；为pH 值时，取±0.2、±0.4、±0.6、±0.8；为温度时，取±0.5℃、±1℃、±1.5℃、±2℃。关于如何求解参数Pi 的灵敏度函数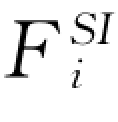，可根据一系列的ΔPi 以及相对应的一系列ΔSI 运用最小二乘法原理，就可得到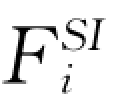的表达式。这样，按照6.2.1.3 节中的有关计算步骤1）～4），可计算出不同参数对饱和指数SI 的“响应”程度，即灵敏度大小，以便从一个侧面为水—岩作用模拟结果的可靠性评价提供依据。

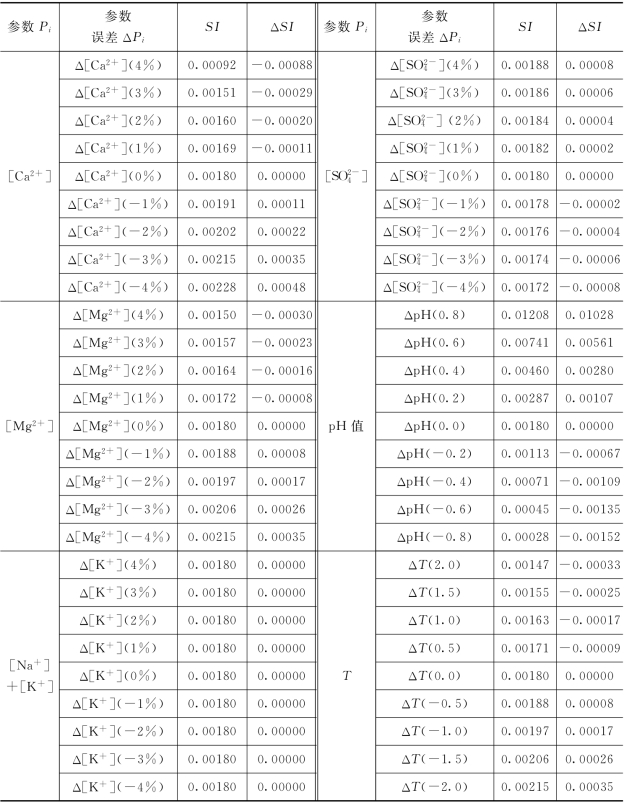
表6.4.2为不同的输入参数Pi 在存在一定比例分析误差ΔPi 的情况下，经计算求得的灌2-3孔位地下水溶液的饱和指数SI 值（反映水与CaCO3 之间的反应状态）统计，表中ΔSum表示各参数Pi（i＝1，2，…，m）同时存在相同的误差。此外，为了对不同的输入参数在相同误差时所造成的饱和指数误差进行分析对比，经计算，亦在该表中列出ΔSI。

表6.4.2　参数误差及其相应的饱和指数SI和饱和指数误差ΔSI统计

续表

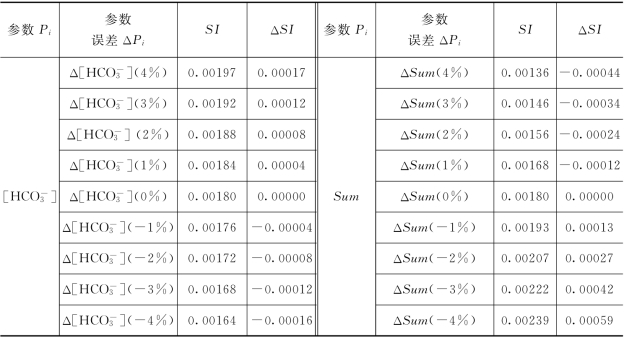
根据表6.4.2可以得出，参数误差ΔSum 所引起的饱和指数误差ΔSI 并不是各单个参数误差所引起的ΔSI 的简单代数和，即：(www.daowen.com)

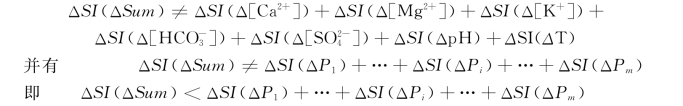
甚至出现ΔSI（ΔSum）小于单个的ΔPi所引起的ΔSI （ΔPi），即ΔSI（ΔSum）＜ΔSI（ΔPi）（i ＝1，2，…，m）。如当误差比例为4%时，由Δ［Ca2＋］所引起的ΔSI 为－0.00088，而由ΔSum 所引起的ΔSI 为－0.00044，后者的绝对值明显小于前者，这些都说明各单个参数误差ΔP1、…、ΔPi、…、ΔPm之间存在耦合作用，反映了不同参数的误差之间存在相互“抵消”的现象，使分析结果比较接近水—岩体系真实的反应状态。

表6.4.3　灵敏度函数表达式及各参数的灵敏度系数统计

6.4.1.3　SI 模型的可信度计算

这里，仍以新安江水电站为例，依据1990～2001 年间的水质分析资料系列，采用Monte Carlo随机分析方法对SI 模型进行可信度分析。

在应用6.2.1.4中有关理论和方法探讨水—岩作用可信度时，需作如下假设：①地下水系统处于化学平衡状态，即水—岩体系为镶嵌平衡体系；②地下水溶液的浓度不是很大，即TDS＜3～6g/L，由此认为该溶液的离子强度小于0.1mol/L；③系统内有关矿物的溶度积常数为已知的确定常数，即不考虑其不确定性。

在进行水与碳酸盐类物质之间反应状态的随机模拟研究中，考虑了各组分的不同存在形式（包括络合物）的浓度，从而得到更能客观反映水—岩作用实际状态的SI 值。有关计算步骤见图6.4.2。

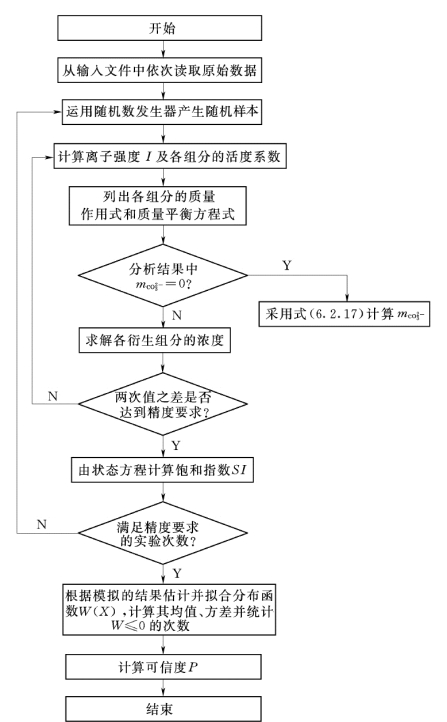
图6.4.2　SI 模型可信度计算流程图

应用基于Monte Carlo方法的随机模拟程序RSSFX.FOR，把表5.2.5中的数据作为输入变量，运行后可分别得到一系列有关方解石和白云石的SI 值。在应用由随机组成的近千组数据的计算过程中，每组数据的电荷不平衡值都在限定的误差范围内。图6.4.3 是灌24-1 水质点模拟次数与收敛曲线，认为选择412 次时的值作为最经济的抽样次数，并且认为计算已经达到精度要求。对于其他水质点的模拟次数也在400 次左右。

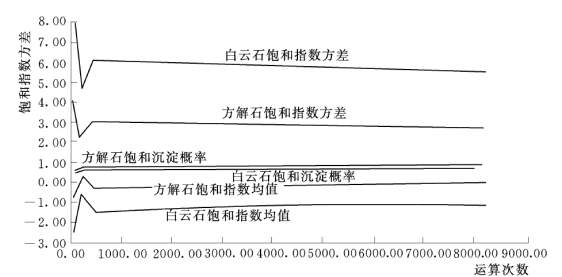
图6.4.3　灌24-1 水质点Monte Carlo模拟次数与各参数收敛曲线

模拟结果（表6.4.4）表明，新安江水电站坝踵帷幕体后灌浆廊道20 个排水孔（水质点）部位具有各不相同的水—岩作用状态，即在各部位方解石和白云石处于溶解状态（或沉淀、平衡状态）的概率不同。在灌3-2、灌4-4、灌5-5、灌7-4、灌9-3、灌16-6、灌17-2、灌19-8、灌21-4等10个孔位方解石和白云石以溶解概率1 而处于完全溶解状态；在灌6-4、灌11 5、灌22-5 等3 个孔位方解石和白云石以溶解概率接近于1 而处于相对溶解状态；在灌12-6、灌23-5、灌24-1 等3 个孔位，方解石和白云石以处于沉淀的概率较大而处于沉淀状态；而在其他孔位（如灌2-3、灌13-5 灌14 6、灌15-6）方解石和白云石处于溶解（或沉淀）的状态介于上述情形之间。沿坝轴线不同坝段地下水溶液中上述碳酸盐类物质的溶解、沉淀或平衡的概率分布曲线见图6.4.4，反映运行条件下区内多数坝段地下水溶液与上述可溶性物质之间处于非饱和状态。这与本章6.4.1.1 一节中采用确定性方法求解SI模型得出的有关结论基本相吻合。

表6.4.4　幕后地下水与方解石、白云石作用状态可信度模拟成果统计

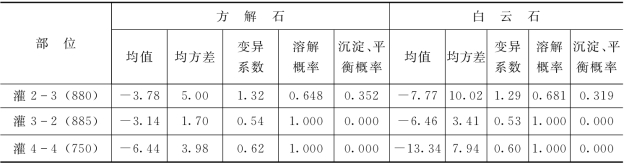
续表

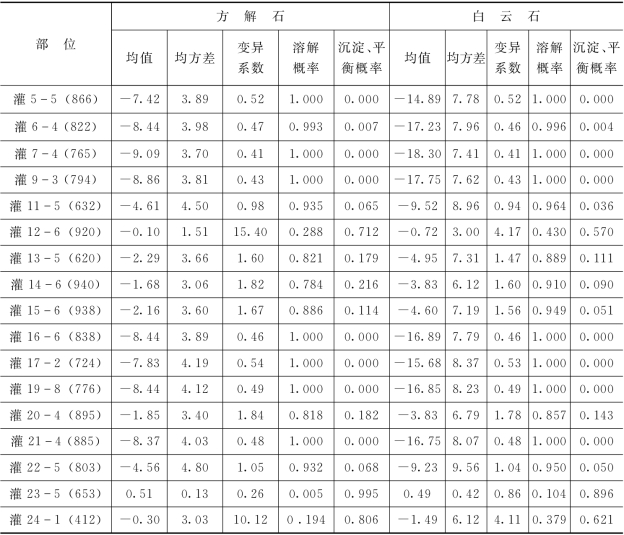
注　表中灌xx指灌浆廊道x坝段x排水孔；括号中数据为迭代次数。

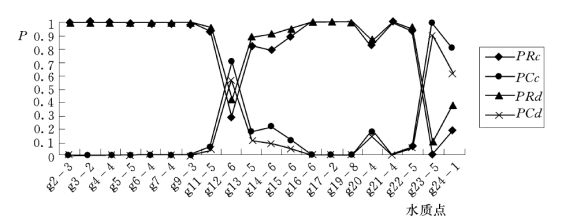
图6.4.4　坝基地下水与碳酸盐类物质之间的反应状态沿坝轴线的分布曲线

PRc—方解石溶解概率；PCc—方解石沉淀概率；PRd—白云石溶解概率；PCd—白云石沉淀概率

如前所述，新安江水电站右坝肩部分坝段基础排水量近年来仍比较大，占坝址总排水量的60%以上。曾在相应部位作了帷幕补强灌浆，虽有大量的水泥浆灌入，但在补强检查孔的岩芯中很少发现水泥结石（彭汉兴等，1994）。可见，该部位地下径流条件较好，以致幕后排水孔位地下水溶液与碳酸盐类物质之间仍处于溶解状态。而在河床—左坝肩部位，基础排水量普遍较小，低于坝址总排水量的40%，反映该部位地下径流滞缓，以致幕后排水孔位地下水溶液与碳酸盐类物质之间相对接近于饱和状态。现场调查发现，出现白色析出物（为碳酸盐类物质）的排水孔也主要位于河床—左坝肩部位。由此表明，上述计算结果总体上是符合实际的，因而是可信的。

上述实例计算结果表明，采用Monte Carlo随机模拟方法对饱和指数SI 模型计算结果的可信度进行量化分析，可以比较有把握地判定有关坝段（或孔位）的水—岩作用状态。即若某部位水—岩作用状态处于溶解（或溶蚀）的概率→1，则相应部位固相介质（包括工程材料等）遭受侵蚀的可能性也就越大；反之，若某部位水—岩作用状态处于溶解的概率→0，则其遭受侵蚀的可能性也就越小。由此可以得出，采用水文地球化学模拟可信度的分析方法是一种较为有效的方法，具有很好的应用前景。由于水质资料的时间系列本身存在不确定性（或随机性）采用上述方法进行模拟，能提供更多的反映水—岩作用状态的有用信息。但方法本身也存在不足之处，如有关模型仍对研究对象做了若干简化假设，没有充分考虑化学动力学方面的影响因素等，因而需要在实践中进一步完善。