5.5.3.1　ARIMA模型的应用

首先，应用本章5.5.1 节建立的ARIMA模型对新安江水电站坝基防渗帷幕体后地下水中Ca2＋离子的浓度进行预测预报。不失一般性，选区内水质监测点——灌13-5 孔为例。利用1990 年第一季度到1999 年第四季度（期间，每年测4次，即每季度测1 次）的数据进行建模，并对2000 年第一季度到2001 年第二季度间对该水质变量进行预测。具体步骤如下。

1.初步确定预测模型的基本形式

如前所述，ARMIA模型是通过数据自身提取各种信息来解释时间序列的变化规律。即一方面可以由其自身的某些滞后序列进行解释，这样可形成AR模型；另一方面也可以由其自身的若干白噪声序列进行解释，这样可形成MA模型。将上述两种模型加以结合就形成了ARIMA模型。考虑到该模型具有时域分析和频域分析的特点，故选此作为预报模型。

2.模型识别

对灌13-5 孔位地下水中Ca2＋时间序列数据先进行统计特征分析，见图5.5.5。图5.5.6 反映，该数据序列分布总体上具有正态性。分别绘制序列不同阶的自相关函数（ACF）图，见图5.5.7、图5.5.9；不同阶的偏自相关函数（PACF）图，见图5.5.8、图5.5.10。

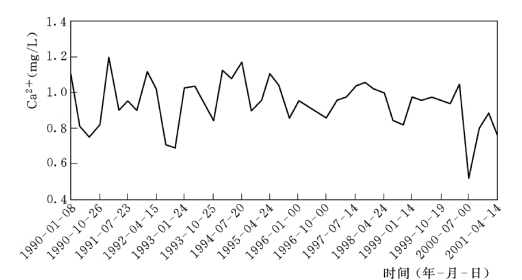
图5.5.5　灌13-5 孔位地下水中Ca2＋时间序列过程线

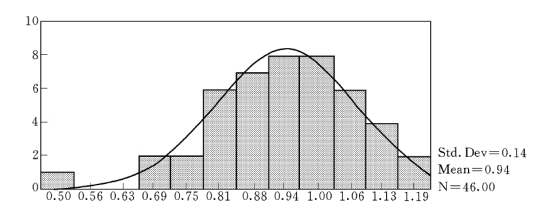
图5.5.6　灌13-5 孔位地下水中Ca2＋变量频数分布直方图

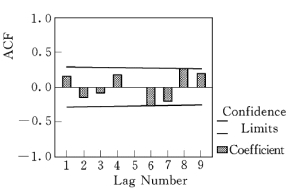
图5.5.7　模型9阶时间序列自相关函数图

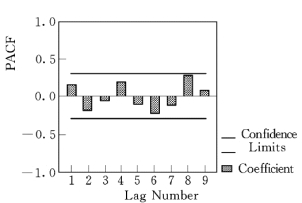
图5.5.8　模型9阶时间序列偏自相关函数图

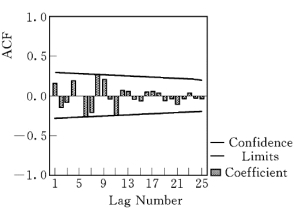
图5.5.9　模型25阶时间序列自相关函数图

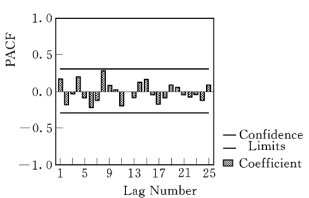
图5.5.10　模型25阶时间序列偏自相关函数图

在ACF图中，时点4、8、12 处有一个高峰；在PACF图中，在时点4、8、12处偏自相关函数也呈高峰，显示该时间序列具有季节性变化因素。因此，应先提取序列的季节性成分，对序列作周期为4的季节性差分，构建的季节性ARIMA模型为（0，1，1）4。然后，提取系列的非季节性成分，作相应残差序列的ACF图（图5.5.11）和PACF图（图5.5.12），构建的非季节性ARIMA模型为（1，1，1）。经拟合，最终得到的模型ARIMA为（1，1，1）× （0，1，1）4。

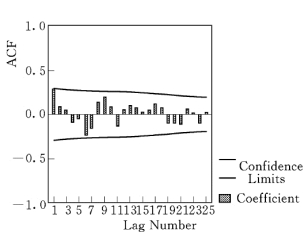
图5.5.11　除季节趋势残差自相关函数图

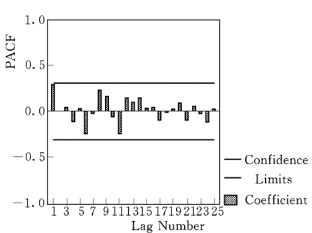
图5.5.12　除季节趋势残差偏自相关函数图

3.参数估计

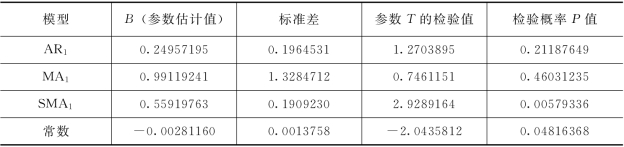
所建模型的参数估计及其检验见表5.5.1。

表5.5.1　模型参数估计值与检验表

模型参数相关系数矩阵：

(www.daowen.com)

由表5.5.1 知，检验概率P 值不大于0.5，反映得到的各参数具有显著水平，且参数之间相关性弱；各参数标准差较小，说明参数估计合理。

4.模型检验

对所建模型ARIMA（p，d，q）×（Sp，Sd，Sq）s 进行残差分析。根据相应残差序列的ACF图（图5.5.13），可知残差的自相关函数值均在可信区间内，说明残差呈随机分布、所含信息基本被提取。因而认为，所建模型是合适的。

5.模型预测

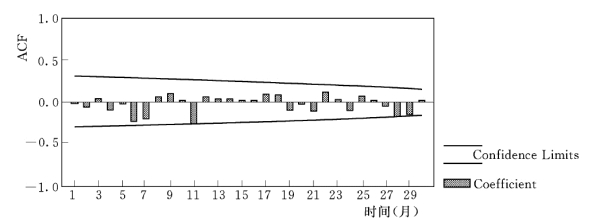
图5.5.13　模型残差的自相关函数图

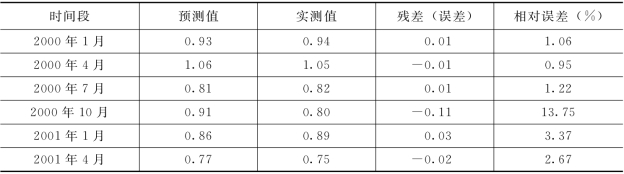
用所建模型对2000年第一季度到2002 年第二季度灌13-5 孔位地下水中Ca2＋离子的含量变化进行预测，有关成果见表5.5.2，有关模型的预测值与实测值之对比曲线见图5.5.14，模型拟合残差曲线见图5.5.15。

表5.5.2　基于ARIMA模型的Ca2＋预测值与实测值对比（mg/L）

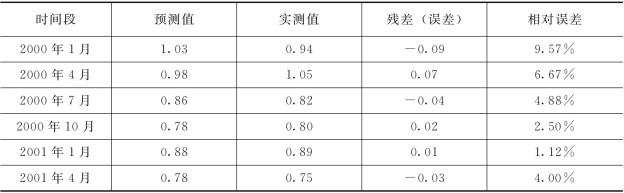
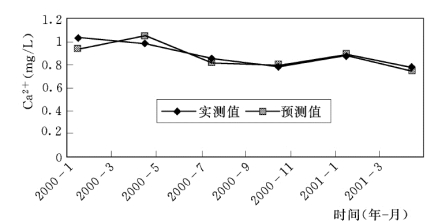
图5.5.14　基于ARIMA模型的Ca2＋预测值与实测值拟合曲线

上述分析表明，应用ARIMA季节性时间序列模型预测坝基帷幕体后地下水中Ca2＋的浓度变化，具有较高的精度。

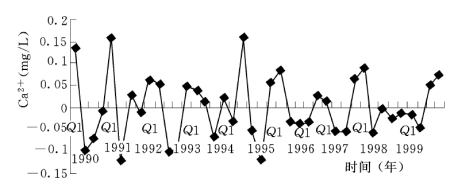
图5.5.15　基于ARIMA模型的Ca2＋拟合残差曲线

5.5.3.2　时间系列混沌模型的应用

应用该模型即相空间神经网络模型，也可对上述工程实例进行计算。其过程如下。

（1）根据灌13-5 孔位地下水中Ca2＋的资料系列计算关联维。利用相空间理论，用自编的VB 程序求该测孔地下水中Ca2＋离子测值序列的关联维，得关联维数d＝5。

（2）确定神经网络的输入数。由所求得的关联维数确定所建立的神经网络。输入为5个：［x（t），x（t－1），x（t－2），x（t－3），x（t－4）］；输出为1个：x（t＋1）。

（3）利用MATLAB神经网络工具箱编写径向基函数神经网络程序，并进行计算。其预测值和实测值拟合曲线见图5.5.16，其残差曲线见图5.5.17。有关计算过程包括如下4个步骤：第1 步，建立网络；第2步，训练网络；第3 步，预测分析；第4步，误差输出。有关计算成果见表5.5.3。根据该表并结合图5.5.16 和图5.5.17可以得到，应用所建模型对实例中灌13-5 孔位地下水中Ca2＋离子含量的预测预报结果能满足精度要求。

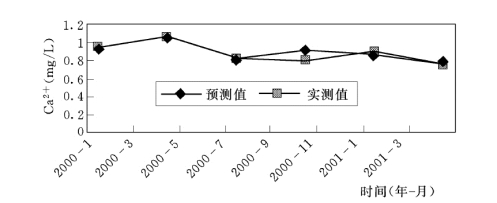
图5.5.16　基于相空间神经网络模型的Ca2＋预测值与实测值拟合曲线

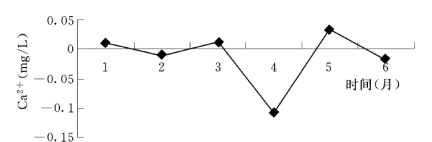
图5.5.17　基于相空间神经网络模型的Ca2＋预测残差曲线

表5.5.3　基于相空间神经网络模型的Ca2＋预测值与实测值（mg/L）对比

还需要指出的是，本章用于预测坝基帷幕体后排水孔位地下水中Ca2＋离子含量变化的相空间径向基函数神经网络模型，是基于观测数据的时间序列客观存在的混沌特性而建立的，根据分维理论可依靠时间序列自身反映其规律和趋势，从而避免了传统BP 神经网络的多因素输入对预测的干扰。由此也表明，大坝基础帷幕体后地下水排泄区（或排泄点如排水孔位）水溶液中有关宏量成分（包括Ca2＋等）的含量随时间的变化确实具有某种混沌特性。

作为小结，应用上述两种模型分别对工程实例中灌13-5 孔地下水中Ca2＋离子于分析时段内的实测数据系列进行了建模，并分别求解作了预测预报。结果表明，两种模型的预测值与实测值之间的误差较小，趋势较吻合。因而认为，其结果能满足精度要求。比较而言，基于相空间神经网络模型的计算精度（除个别测点）总体上要高于ARIMA模型。